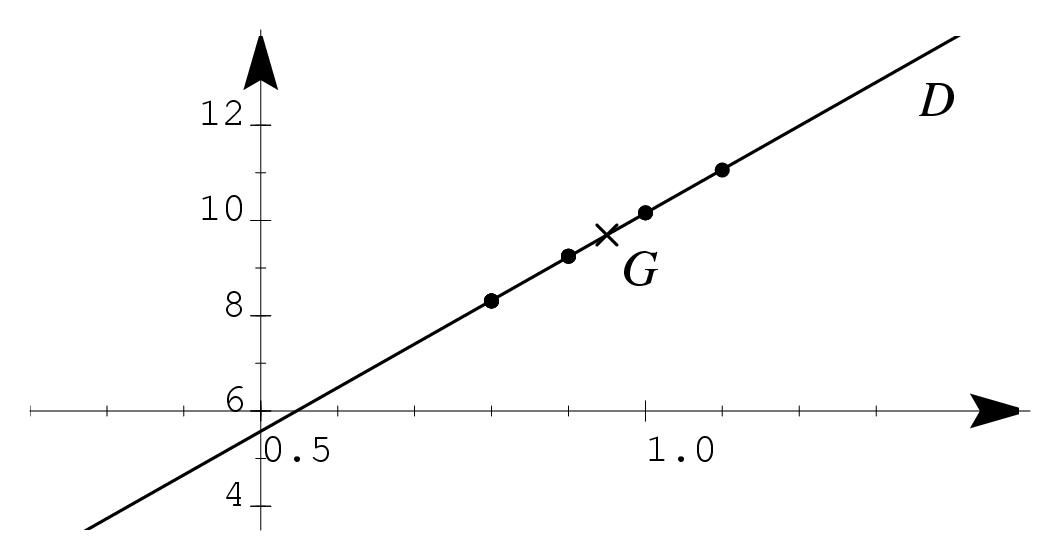
\exo{Méthode des moindres carrés~: Coefficient de diffusion} Lorsque l'on maintient en contact deux blocs de métal à haute température, les deux blocs se soudent au bout d'un certain temps, des atomes d'un bloc s'étant déplacés sur l'autre et réciproquement~: on dit alors qu'il y a {\sl diffusion}. Le but de ce problème est d'étudier la variation du coefficient de diffusion $D$ (exprimé en cm.s$^{-1}$) en fonction de la température $T$ (exprimée en degrés Kelvin). On étudie expérimentalement la diffusion de l'or irradié~198 dans l'or stable. On pose $$ X = {10^3 \over T} \qquad {\rm et} \qquad Y = - \log D $$ où $\log$ désigne le logarithme décimal (c'est à dire que $\log D = {\ln D \over \ln 10}$ où $\ln$ désigne le logarithme népérien). On obtient expérimentalement le tableau suivant~: $$\vbox{\halign{ \offinterlineskip %% preamble #\tv && \cc{$#$}& #\tv \cr \noalign{\hrule} & X_i&& 0, 8&& 0, 9&& 1&& 1, 1& \cr \noalign{\hrule} & Y_i && 8, 31&& 9, 25&& 10, 16&& 11, 06& \cr \noalign{\hrule} }}$$ \itemnum Représenter graphiquement le nuage de points $(X_i, Y_i)$. \itemnum Calculer les coordonnées du point moyen de ce nuage. \itemnum Déterminer la valeur approchée à $10^{-3}$ près du coefficient de corrélation linéaire de la série statistique de variables $X$ et $Y$. Interpréter votre résultat. \itemitemalphnum Déterminer l'équation réduite de $D$, la droite de régression de $Y$ en $X$ par la méthode des moindres carrés. Les coefficients seront donnés à $10^{-2}$ près. \itemitemalph Tracer la droite $D$ sur le graphique. \itemitemalphnum Déduire de la question précédente l'existence de deux réels strictement positifs $\alpha$ et $\beta$, que l'on déterminera avec deux chiffres significatifs, tels que $$ D = \alpha e^{- \beta /T}. $$ \itemitemalph Dresser le tableau des valeurs de $D$ (avec deux chiffres significatifs) associés aux valeurs de $T$ suivantes~: $900$, $1\, 000$, $1\, 100$, $1\, 200$ et $1\, 300$. \finexo \corrige{} \def \epspath{% $HOME/tex_doc/lycee/database/btsmai/stats/} %\epsfxsize = 80mm \rightsuperboxepsillustrate{reg_005.ps}{-15} \advance \numno by 1 \num\ Pour le point moyen, on calcule la moyen\-ne a\-ri\-thmé\-ti\-que de chacun des caractères. On trouve ainsi $$ \dresultat{G~: ( 0, 95\ ; 9, 695)} $$ \num\ On trouve successivement $$ \overline X = 0, 95\ ; \qquad \sigma (X) \simeq 0,112\ ; $$ % \qquad {\rm et} \qquad et $$ \overline Y \simeq 9, 695\ ; \qquad \sigma (Y) \simeq 1, 024 $$ Le calcul de la covariance et du coefficient de cor\-ré\-la\-tion linéaire par les formules $$ \sigma_{XY} = {1\over n} \left( \sum_{i=1}^n X_iY_i\right) - \overline X\overline Y, \qquad {\rm et} \qquad r = {\sigma_{XY} \over \sigma (X) \times \sigma (Y)} $$ donne alors $$ \dresultat{\sigma_{XY} \simeq 0, 114\, 5}\ ; \qquad {\rm et} \qquad \dresultat{r \simeq 0,999} $$ Le coefficient de corrélation étant plutôt \og bon\fg\ (ie \og proche\fg\ de~1), \tresultat {une approximation affine paraît adaptée.} \num\ La droite $D$ de régression de $Y$ en $X$ possède une équation de la forme $Y = aX+b$, où $a$ et $b$ vérifient $$ a = {\sigma_{XY} \over [\sigma (X)]^2}, \quad {\rm soit} \quad \dresultat{a \simeq {0, 114\, 5 \over 0,012\,5} \simeq 9,16} \qquad {\rm et} \qquad \overline Y = a \overline X + b, \quad {\rm soit} \quad \dresultat{b \simeq 0, 993} $$ d'où l'équation cherchée~: \mresultat{D: Y = 9,16 X + 0, 993} \alphnum\ En substituant, dans l'équation précédente, $10^3/T$ à $X$ et $-(\ln D) / (\ln 10)$ à $Y$, il vient~: $$\displaylines{ Y = 9,16 X + 0, 993 \quad \Longleftrightarrow \quad -{\ln D \over \ln 10} = 9,16 \times {10^3 \over T} + 0, 993 \cr \ln D = - (\ln 10) \times \left( {9, 16.10^3 \over T} + 0, 993\right) \quad \Longleftrightarrow \quad D = e^{-(\ln 10) \times \left( {9, 16.10^3 \over T}\right) - (\ln 10) \times 0, 993} \cr {\rm d'où} \quad D = {e^{-(\ln 10) \times 9, 16.10^3 / T} \over e^{(\ln 10) \times 0, 993}} = \alpha e^{-\beta /T} \cr {\rm avec} \qquad \dresultat{\alpha = 1 / e^{(\ln 10) \times 0, 993} \simeq 0, 102} \qquad {\rm et} \qquad \dresultat{\beta = (\ln 10) \times 9, 16.10^3 \simeq 20\, 091, 68} }$$ \alph\ Avec ces valeurs pour $\alpha$ et $\beta$, on trouve alors $$\vbox{\halign{ \offinterlineskip %% preamble #\tv && \cc{$#$}& #\tv \cr \noalign{\hrule} & T&& 900&& 1\, 000&& 1\, 100&& 1\, 200&& 1\, 300& \cr \noalign{\hrule} & D&& 6, 75.10^{-12}&& 7, 03 . 10^{-11}&& 4, 78.10^{-11}&& 2, 36.10^{-9}&& 9, 14.10^{-9}& \cr \noalign{\hrule} }}$$ \fincorrige