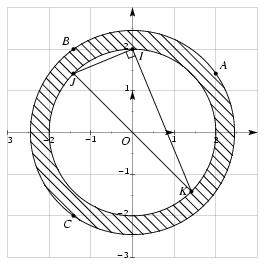
\exo {\' Equation du second degré, géométrie. {\sl bac sti gm, 2000}} Le plan complexe est muni d'un repère orthonormal $(O, \vec u, \vec v)$ d'unité graphique $2$~cm (ou $2$~grands carreaux). On désigne par $A$ le point d'affixe $$ z_A = 2 + i\sqrt 2. $$ \itemitemalphnum Résoudre dans l'ensemble des nombres complexes l'équation~: $$ z^2 + 2\sqrt 2 z + 6 = 0. $$ On appelle $z_B$ la solution de cette équation dont la partie imaginaire est positive. \itemitemalph Placer dans le plan complexe les points $A$ et $B$ d'affixes respectives $z_A$ et $z_B$. \itemnum Montrer que les points $A$ et $B$ appartiennent au cercle $\cal C$ de centre $O$ et de rayon $\sqrt 6$. \itemnum Soient $I$, $J$ et $K$ les points d'affixes respectives $z_I$, $z_J$ et $z_K$ telles que~: \itemitem {$\bullet $} $z_I = 2i$~; \itemitem {$\bullet $} $z_J$ est le nombre complexe de module $2$ et d'argument $3\pi / 4$. \itemitem {$\bullet $} $z_K = -z_J$. \itemitemalph Donner la forme algébrique de $z_J$. \itemitemalph Placer les points $I$, $J$ et $K$ dans le plan complexe. \itemitemalph Quelle est la nature du triangle $IJK$~? Justifier. \itemitemalph Donner le rayon du cercle ${\cal C}'$ circonscrit au triangle $IJK$. \itemnum Soit $E$ l'ensemble des points $M$ du plan dont l'affixe $z$ vérifie la relation~: $$ 2 < |z| < \sqrt 6. $$ \itemitemalph Tracer les cercles $\cal C$ et ${\cal C}'$. \itemitemalph Représenter l'ensemble $E$ sur le graphique précédent à l'aide de hachures. Justifier \finexo \corrige \itemalphnum On trouve $\Delta = -16$, d'où les deux racines complexes conjuguées $$ z_B = {-2\sqrt 2 + 4i \over 2} = \dresultat {-\sqrt 2 + 2i = z_B} \qquad {\rm et} \qquad \dresultat {z_C = -\sqrt 2 - 2i}. $$ \def \epspath {% $HOME/tex_doc/lycee/database/term/sti/algebre/complex/} \itemalph $$ \epsillustrate {equ2_004.ps} $$ \itemnum On a $|z_A| = \sqrt {2^2 + (\sqrt 2)^2}$, soit $|z_A| = \sqrt 6$ et $|z_B| = \sqrt 6$, donc \dresultat {OA = OB = \sqrt 6}, ce qui prouve que les points \tresultat {$A$ et $B$ sont sur le cercle de centre $O$ de rayon $\sqrt 6$}. \itemalphnum On a $$\displaylines { z_J = 2 e^{3i\pi / 4} = 2 \left( \cos \left( 3\pi \over 4\right) + i\sin \left( {3\pi \over 4}\right)\right) = 2 \left( -{\sqrt 2 \over 2} + i{\sqrt 2 \over 2}\right) \cr {\rm soit} \qquad \dresultat {z_J = -\sqrt 2 + i \sqrt 2}. \cr }$$ \advance \alphno by 1 \itemalph Calculons les longueurs des côtés du triangle $IJK$. Il vient $$\displaylines { IJ = |z_J - z_I| = |-\sqrt 2 + i (\sqrt 2 - 2)| = \sqrt {8 - 4\sqrt 2} \qquad \qquad JK = |z_K - z_J| = |2\sqrt 2 - 2i\sqrt 2| = \sqrt {16} \cr {\rm et} \qquad IK = |\sqrt 2 + i (-\sqrt 2 - 2)| = \sqrt {8 + 4\sqrt 2}. \cr }$$ On a alors évidemment $IJ^2 + IK^2 = JK^2$, et le théorème de Pythagore permet de conclure que le triangle \tresultat {$IJK$ est rectangle en $I$}. \itemalph On a $$ |z_I| = |2i| = 2, \qquad \qquad |z_J| = |-\sqrt 2 + i\sqrt 2| = 2 \qquad \qquad |z_K| = |\sqrt 2 - i\sqrt 2| = 2 $$ d'où l'on déduit que les points $I$, $J$ et $K$ sont tous situés sur le même cercle de centre $O$ et \tresultat {de rayon $2$}. Ce cercle est donc le cercle circonscrit au triangle $IJK$. \itemnum \advance \alphno by 1 \alph \ L'ensemble des points $M$ dont l'affixe $z$ vérifie la relation $$ 2 < |z| < \sqrt 6 $$ est l'ensemble des points $M$ tels que la distance $OM$ vérifie la relation $$ 2 < OM < \sqrt 6. $$ On en déduit que cet ensemble est \tresultat {la couronne circulaire comprise entre $\cal C$ et ${\cal C}'$} \fincorrige