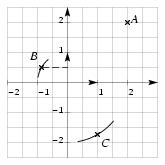
\exo{posé au bac ({\sl STI GM, 1996})} Soient les nombres complexes $$ z_1 = 2 + 2i, \qquad z_2 = e^{5i\pi /6}, \qquad {\rm et} \qquad z_3 = 1 - i\sqrt3. $$ \itemnum Déterminer le module et un argument de $z_1$, $z_2$ et $z_3$. \itemnum Le plan est rapporté à un repère orthonormal $(O, \vec u, \vec v)$ d'unité graphique 2~cm (ou 2~grands carreaux). \itemitemalph Placer le point $A$ d'affixe $z_1$. \itemitemalph En utilisant les résultats de la question {\bf 1.}, que l'on fera apparaître sur la figure, placer les points $B$ et $C$ d'affixes respectives $z_2$ et $z_3$. \itemitemalphnum Déterminer les nombres réels $a$ et $b$ tels que $z_2 = a + bi$. \itemitemalph Montrer que $\displaystyle { z_1 \times z_2 = - \big( 1 + \sqrt3 \big) + i \big( 1 - \sqrt3 \big) }$. \itemitemalph Déterminer la forme exponentielle de $z_1 \times z_2$. \itemitemalph Utiliser les résultats précédents pour donner les valeurs exactes de $$ \cos \Big( {13 \pi \over 12} \Big) \qquad {\rm et} \qquad \sin \Big( {13 \pi \over 12} \Big). $$ \finexo \corrige \itemnum On a $|z_1| = \sqrt {4+4} = 2\sqrt 2$ d'où $\cos \theta _1 = \sqrt 2/2$ et $\sin \theta _1 = \sqrt 2/2$. On en déduit $\theta _1 = \pi /4$. Finalement, on a $$\dresultat { z_1 = \left[ 2\sqrt 2, {\pi \over 4}\right] = 2\sqrt 2 e^{i\pi /4} }$$ \item {} On lit immédiatement $|z_2| = 1$ et $\theta _2 = 5\pi /6$. Soit $$\dresultat { z_2 = \left[ 1, {5\pi \over 6}\right] = e^{5i\pi /6} }$$ \item {} Et pour $z_3$ on trouve $|z_3| = \sqrt {1 + 4} = 2$, $\cos \theta _3 = 1/2$ et $\sin \theta _3 = -\sqrt 3 / 2$. On en déduit $$\dresultat { z_3 = \left[ 2, - {\pi \over 3}\right] = 2e^{-i\pi /3} }$$ \def \epspath {% $HOME/tex_doc/lycee/database/term/sti/algebre/complex/} \itemnum $$ \superboxepsillustrate {exo_009.ps} $$ \itemalphnum On sait que $r e^{i\theta } = r \big( \cos \theta + i \sin \theta \big) $. On a donc facilement $$\dresultat { z_2 = - {\sqrt 3\over 2} + {1\over 2} i }$$ \itemalph En calculant ce produit sous forme algébrique, on trouve $ z_1 \times z_2 = (2 + 2i) \times {1\over 2} (-\sqrt 3 + i) = (1 + i) \times (-\sqrt 3 + i) $, soit \dresultat {z_1 \times z_2 = - \big( 1 + \sqrt3 \big) + i \big( 1 - \sqrt3 \big) }. \itemalph Et en reprenant ce calcul, mais sous forme trigonométrique, on trouve $$\eqalign { z_1 \times z_2 = \left[ 2\sqrt 2, {\pi \over 4}\right] \times \left[ 1, {5\pi \over 6}\right] &= \left[ 1 \times 2\sqrt 2, {\pi \over 4} + {5\pi \over 6}\right] \cr \qquad &{\rm soit} \qquad \dresultat { z_1 \times z_2 = \left[ 2\sqrt 2, {13\pi \over 12}\right] = = 2\sqrt 2 e^{13i\pi \over 12} } }$$ \itemalph En identifiant ces deux derniers résultats, il vient $$ 2\sqrt 2 \times \left( \cos {13\pi \over 12} + i \sin {13\pi \over 12}\right) = - \big( 1 + \sqrt3 \big) + i \big( 1 - \sqrt3 \big) $$ d'où, en identifiant maintenant les parties réelles et imaginaires, $$ \dresultat {\cos {13\pi \over 12}= {- 1 - \sqrt 3\over 2\sqrt 2 }} \qquad {\rm et} \qquad \dresultat {\sin {13\pi \over 12}= {1 - \sqrt 3\over 2\sqrt 2 }} $$ \fincorrige