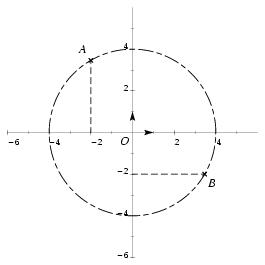
\exo{\'Equation du second degré dans $\cset$, géométrie. {\sl bac sti gm, sept. 96}} On désigne par $i$ le nombre complexe de module~1 et d'argument $\pi/2$. \itemitemalphnum Résoudre dans $\cset$ l'équation d'inconnue $z$~: $$ z^2 + 4z + 16 = 0. $$ On note $z_1$ et $z_2$ les solutions de cette équation, $z_1$ désigne celle dont la partie imaginaire est positive. \itemitemalph Déterminer le module et un argument de chacune de ces solutions. \itemnum Le plan complexe est rapporté à un repère orthogonal direct $(O, \vec u, \vec v)$ d'unité graphique 1~cm (ou 1~grand carreau). On appelle $A$ et $B$ les points d'affixes respectives $z_1$ et $i\times z_2$. \itemitemalph Calculer $i \times z_2$. En déduire les coordonnées du point $B$. \itemitemalph Sans utiliser de valeurs approchées, placer dans le plan complexe les points $A$ et $B$ (justifier la construction). \itemnum Soit $M$ un point quelconque d'affixe $z$ dans le plan complexe. \itemitemalph Interpréter géométriquement le module $|z - z_1|$ du nombre complexe $z - z_1$. \itemitemalph Déterminer l'ensemble $(\Delta)$ des points $M$ du plan dont l'affixe $z$ est telle que $$ |z - z_1| = |z - iz_2|. $$ \itemitemalph Construire l'ensemble $(\Delta)$ sur la figure. \finexo \corrige {} \itemalphnum On trouve $\Delta = -48 = \left( 4i\sqrt 3\right) ^2 < 0$. On a donc 2~racines complexes conjuguées~: $$ \dresultat {z_1 = {-4+4i\sqrt 3 \over 2} = -2 + 2i\sqrt 3} \qquad {\rm et} \qquad \dresultat {z_2 = -2 - 2i\sqrt 3} $$ \itemalph On trouve facilement $|z_1| = |z_2| = 4$, d'où $$ \cases { \cos \theta _1 = -1/2 \cr \sin \theta _1 = \sqrt 3 /2 \cr } \Rightarrow \theta _1 = {2\pi \over 3} + 2k\pi \qquad {\rm et} \qquad \cases { \cos \theta _2 = -1/2 \cr \sin \theta _2 = -\sqrt 3 /2 \cr } \Rightarrow \theta _2 = -{2\pi \over 3} + 2k\pi $$ On a donc finalement \dresultat {z_1 = \left[ 4, {2\pi \over 3}\right] = 4 e^{2i\pi /3}} et \dresultat {z_2 = \left[ 4, -{2\pi \over 3}\right] = 4 e^{-2i\pi /3}} \itemalphnum On trouve $iz_2 = 2\sqrt 3 - 2i$. Le point $B$ a donc pour coordonnées \dresultat {B (2\sqrt 3, -2)}. \def \epspath {% $HOME/tex_doc/lycee/database/term/sti/algebre/complex/} \itemalph Pour placer le point $B$ avec une construction exacte, il est nécessaire de déterminer la forme trigonométrique de $z_B$. On trouve \dresultat {z_B = 2\sqrt 3 - 2i = 4e^{-i\pi /6}}. \epsfxsize 80mm $$ \superboxepsillustrate {exo_012.ps} $$ \fincorrige