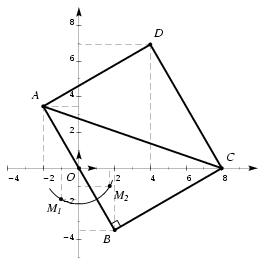
\exo{Module, argument, application à la géométrie ({\sl bac Gm 97\/})} Le plan complexe $\cal P$ est rapporté au repère orthonormal $(O, \vec u, \vec v)$ d'unité graphique 1~cm (ou 1~grand carreau). On note $i$ le nombre complexe de module~1 et d'argument~$\pi/2$, et $z_1$ le nombre complexe $$ z_1 = -1 -i\sqrt3. $$ \itemnum On pose $z_2 = iz_1$. Montrer que \quad $z_2 = \sqrt3 - i$. \itemitemalphnum Calculer le module et un argument de chacun des nombres complexes $z_1$ et $z_2$. \itemitemalph Placer dans le plan $\cal P$ le point $M_1$ d'affixe $z_1$ et le point $M_2$ d'affixe $z_2$. \itemnum Soient $A$, $B$ et $C$ les points du plan d'affixes respectives $z_A$, $z_B$ et $z_C$ telles que~: $$ z_A = -2 + 2i\sqrt3, \qquad z_B = 2 - 2i\sqrt3, \qquad {\rm et} \qquad z_C = 8. $$ \itemitemalph Montrer que $z_A = 2\overline {z_1}$ et que $z_B = -z_A$. \itemitemalph Placer les points $A$, $B$ et $C$ dans le plan $\cal P$. \itemitemalph Démontrer que le triangle $ABC$ est rectangle. \itemitemalph Calculer l'affixe du point $D$ de sorte que le quadrilatère $ABCD$ soit un rectangle. \finexo \corrige{} \itemnum On a $z_2 = i z_1 = -i -i^2 \sqrt3$, soit \mresultat{z_2 = \sqrt3 - i} puisque $i^2 = -1$. \itemalphnum On a $|z_1| = \sqrt{(-1)^2 + (\sqrt3)^2}$, soit \mresultat{|z_1| = 2}. On trouve de la même façon \mresultat{|z_2| = 2}. On a alors $$ \cases{ \cos \theta_1 = -1/2 \cr \sin \theta_1 = -\sqrt3/2 \cr} \quad {\rm d'où} \quad \dresultat{\theta_1 = -{2\pi \over3}} \qquad {\rm et} \qquad \cases{ \cos \theta_2 = \sqrt3/2 \cr \sin \theta_2 = -1/2 \cr} \quad {\rm d'où} \quad \dresultat{\theta_2 = -{\pi \over6}} $$ \itemalphnum Il est évident que \mresultat{z_B = -z_A}, et comme $\overline {z_1} = -1+i\sqrt3$, on a facilement \mresultat{z_A = 2\overline {z_1}}. \def \epspath{% $HOME/tex_doc/lycee/database/term/sti/algebre/complex/} \epsfxsize = 80mm \itemalph $$ \superboxepsillustrate{geom_002.ps} $$ \itemalph On a $$\displaylines{ AB = |z_B - z_A| = |4 - 4i\sqrt3| = \sqrt{64} = 8, \qquad AC = |z_C - z_A| = |10 - 2i\sqrt3| = \sqrt{112} = 4\sqrt7, \cr {\rm et} \qquad BC = |z_C - z_D| = |6 + 2i\sqrt3| = \sqrt{48} = 4\sqrt3. \cr }$$ Donc \tresultat{$ABC$ rectangle en $B$} par Pythagore puisque $AC^2 = AB^2 + BC^2$. \itemalph Pour que $ABCD$ soit un rectangle, il suffit que ce soit un parallélogramme (puisque l'on a déjà un triangle rectangle). Il suffit donc d'avoir $\overrightarrow{AB} = \overrightarrow{DC}$, autrement dit $z_B - z_A = z_C - z_D$. Ce qui donne finalement $z_D = z_C - z_B + z_A$. D'où l'affixe cherché~: \mresultat{z_D = 4 + 4i\sqrt3} et les coordonnées du point $D$~: $D (4, 4\sqrt3)$. \fincorrige