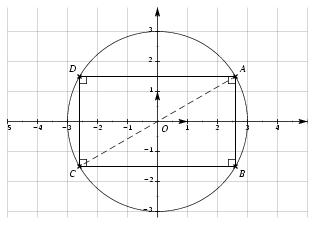
\exo {Complexes et géométrie} Tous les résultats seront justifiés. On considère les nombres complexes $$ z_1 = 3\left( \cos {\pi \over 6} + i \sin {\pi \over 6}\right), \qquad \qquad z_2 = \overline {z_1}, \qquad \qquad z_3 = -z_1 \qquad \qquad z_4 = z_1 e^{2i\pi \over 3}, $$ où $\overline {z_1}$ désigne le nombre complexe conjugué de $z_1$. \itemnum Déterminer la forme algébrique des nombres complexes $z_1$, $z_2$ et $z_3$. \itemnum Déterminer le module et un argument des nombres complexes $z_2$ et $z_3$. \itemitemalphnum Montrer que $$ z_4 = 3e^{5i\pi \over 6} $$ \itemitemalph En déduire le module et un argument du nombre complexe $z_4$. \itemitemalph Quelle est la forme algébrique de $z_4$~? \itemnum Le plan complexe est rapporté à un repère orthonormé $(O, \vec u, \vec v\/)$ (unité graphique~: $2\cm $). On considère les points $A$, $B$, $C$ et $D$ d'affixes respectives $z_1$, $z_2$, $z_3$ et $z_4$. \itemitemalph Montrer que les points $A$, $B$, $C$ et $D$ sont sur un même cercle dont on précisera le centre et le rayon. Construire ce cercle. \itemitemalph Construire les points $A$, $B$, $C$ et $D$ en utilisant leurs ordonnées. \itemitemalph Calculer les distances $AC$ et $BD$. \itemitemalph Quelle est la nature du quadrilatère $ABCD$~? \finexo \corrige \itemnum Il vient $$ z_1 = 3\left( \cos {\pi \over 6} + i \sin {\pi \over 6}\right) = 3\left( {\sqrt 3 \over 2} + {1 \over 2}i\right) \quad {\rm soit} \quad \dresultat {z_1 = {3\sqrt 3 \over 2} + {3 \over 2}i} $$ On a alors facilement $$ \dresultat {z_2 = {3\sqrt 3 \over 2} - {3 \over 2}i} \quad {\rm soit} \quad \dresultat {z_3 = -{3\sqrt 3 \over 2} - {3 \over 2}i} $$ \itemnum On a évidemment $z_1 = \big[ 3 ; {\pi \over 6}\big] $. En utilisant les propriétés du conjugué, on a alors \dresultat {z_2 = \Big[ 3 ; -{\pi \over 6}\Big] }. \item {} Pour $z_3$, on pourrait procéder de la même façon en utilisant le fait que $-1 = \big[ 1; \pi\big] , $ puis en utilisant les propriétés de la multiplication de complexes sous forme trigonométrique. Utilisons la méthode choisie par la plupart d'entre vous~: $$ |z_3| = \sqrt {\left( {3\sqrt 3}\over 2\right) ^2 + \left( {3\over 2}\right) ^2} = \sqrt {{27\over 4} + {9\over 4}} = {6\over 2} = 3 \quad {\rm d'où} \quad \cases { \cos \theta _3 = -{\sqrt 3\over 2} \cr \sin \theta _3 = -{1\over 2} \cr } \quad \Longrightarrow \quad \theta _3 = -{5\pi\over 6} \quad {\rm convient} $$ Finalement \dresultat {z_3 = \Big[ 3 ; -{5\pi \over 6}\Big] }. \itemalphnum Il vient $$ z_4 = z_1 e^{2i\pi \over 3} = 3 e^{i\pi \over 6} e^{2i\pi \over 3} = 3 e^{{i\pi \over 6} {2i\pi \over 3}} = \dresultat {3 e^{{5i\pi \over 6}} = z_1} $$ \itemalph On a bien sûr \dresultat {|z_4| = 3} et \dresultat {\arg z_4 = {5\pi \over 6}} . \itemalph D'où $$ z_4 = 3\left( \cos {5\pi \over 6} + i \sin {5\pi \over 6}\right) = 3\left( -{\sqrt 3 \over 2} + {1 \over 2}i\right) \quad {\rm soit} \quad \dresultat {z_4 = -{3\sqrt 3 \over 2} + {3 \over 2}i} $$ %% \itemalphnum On a, d'après les questions précédentes, $|z_1| = |z_2| = %% |z_3| = |z_4| = 3$, donc $OA = OB = OC = OD = 3$, ce qui prouve %% que les points $A$, $B$, $C$ et $D$ sont sur un \tresultat {même cercle de %% centre $O$ et de rayon $3$}. %% %% \def \epspath {% %% $HOME/tex_doc/lycee/database/term/sti/algebre/complex/} %% \itemalph %% $$ %% \superboxepsillustrate {geom_009.ps} %% $$ %% %% \catcode`|=12 %% \itemalph Il vient %% $$ %% AC = |z_3 - z_1| %% = \left| -{3\sqrt 3 \over 2} - {3 \over 2}i - {3\sqrt 3 \over 2} - {3 \over 2}i\right| %% = \left| -3\sqrt 3 - 3i\right| %% = \sqrt {\left( 3\sqrt 3\right) ^2 + 3^2} %% = \dresultat {6 = AC} %% $$ %% De la même manière, %% $$ %% BD = |z_4 - z_2| %% = \left| -{3\sqrt 3 \over 2} + {3 \over 2}i - {3\sqrt 3 \over 2} + {3 \over 2}i\right| %% = \left| -3\sqrt 3 + 3i\right| %% = \sqrt {\left( 3\sqrt 3\right) ^2 + 3^2} %% = \dresultat {6 = BD} %% $$ %% %% \itemalph Le quadrilatère $ABCD$ est inscrit dans un cercle de centre %% $O$ et de rayon 3. On sait que $AC = 6$, ce qui prouve que %% $[AC]$ est un diamètre de ce cercle, donc les triangles $ABC$ %% et $ABD$ sont respectivement rectangles en $B$ et en $D$. Un %% raisonnement analogue à partir de la relation $BD = 6$ prouve %% que les triangles $BCD$ et $BAD$ sont respectivement rectangles %% en $C$ et en $A$. Ce qui prouve que \tresultat {$ABCD$ est un %% rectangle}. \fincorrige