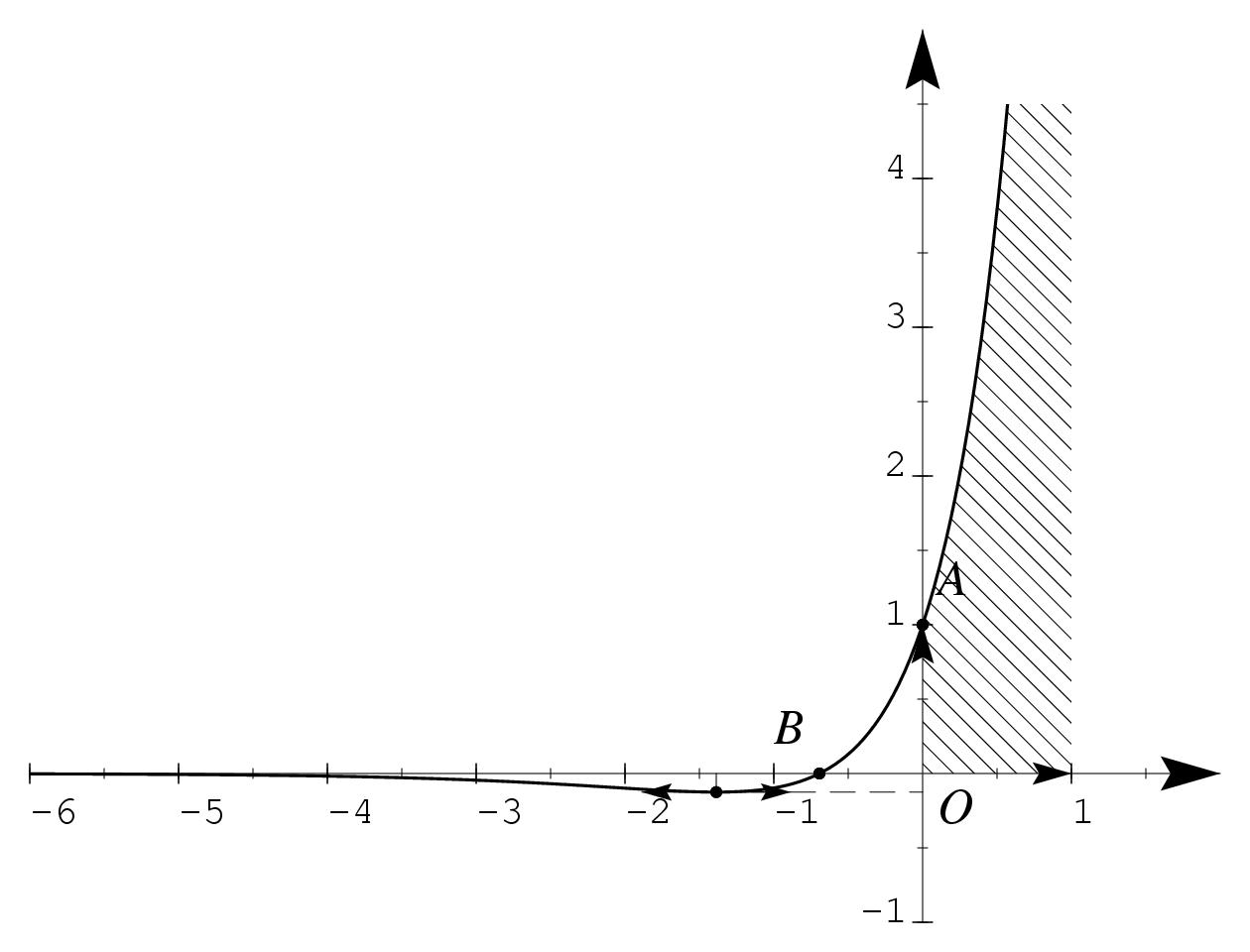
\exo{Une équation différentielle d'ordre 1} On considère les équations différentielles $$ (E_1):y'-2y=0 \qquad {\rm et} \qquad (E_2):y'=y. $$ \itemitemalphnum Résoudre les équations différentielles $(E_1)$ et $(E_2)$. \itemitemalph Déterminer la solution particulière $f_1$ de $(E_1)$ telle que $f'_1 (0)=4$ \itemitem{} Déterminer la solution particulière $f_2$ de $(E_2)$ telle que $f_2 (0)=1$. \itemnum Soit $g$ la fonction définie sur $\rset$ par~: \quad $g(x)=2e^{2x}-e^x$. \itemitemalph \'Etudier les limites de la fonction $g$ en $-\infty $ et en $+\infty $. Pour étudier la limite de $g$ en $+\infty$, on pourra écrire, pour tout nombre réel $x$, $g(x)=e^x(2e^x-1)$. \itemitemalph Déduire de la question précédente l'existence d'une asymptote dont on précisera une équation. \itemitemalph Déterminer la dérivée $g'$ de $g$. \itemitemalph \'Etudier le signe de $g'$. En déduire le tableau des variations de $g$. \itemnum Préciser les coordonnées des points d'intersection de la courbe avec les axes du repère. \itemnum Construire la courbe représentative de la fonction $g$ dans un repère orthogonal. \itemnum Déterminer, en unités d'aire, l'aire comprise entre la courbe de $g$, l'axe $Ox$ et les droites d'équations respectives $x = 0$ et $x = 1$. \finexo \corrige{} \itemalphnum Le cours nous dit que~ \item{$\bullet $} Les solutions de l'équation $(E_1)$ sont toutes les fonctions $y$ ayant une écriture de la forme \dresultat{y (x) = k e^{2x}}, où $k$ est une constante réelle quelconque. \item{$\bullet $} Les solutions de l'équation $(E_2)$ sont toutes les fonctions $y$ ayant une écriture de la forme \dresultat{y (x) = \ell e^{x}}, où $\ell $ est une constante réelle quelconque. \itemalph Si $f_1$ est solution de $(E_1)$, alors $f_1 (x)$ s'écrit $f_1 (x) = k e^{2x}$ pour une certaine valeur de $k$. On a donc $f'_1 (x) = 2ke^{2x}$, et $f'_1 (0) = 2k$. De la condition initiale $f'_1 (0) = 4$, on en déduit alors que $k = 2$. D'où la fonction cherchée \mresultat{f_1 (x) = 2 e^{2x}}. \item{} De la même façon, si $f_2$ est solution de $(E_2)$, alors $f_2 (x)$ s'écrit $f_2 (x) = \ell e^x$ pour une certaine valeur de $\ell $. De la condition initiale $f_2 (0) = 1$, on en déduit alors que $\ell = 1$. D'où la fonction cherchée \mresultat{f_2 (x) = e^x}. \everymath = {\displaystyle } \itemalphnum On a facilement \dresultat{\lim_{x \to -\infty } g (x) = 0} puisque $g (x) = 2e^{2x} - e^x$ avec $\lim_{x \to -\infty } e^{2x} = 0$ et $\lim_{x \to -\infty } e^x = 0$. \item{} En $+\infty $, l'écriture $2e^{2x} - e^x$ donne une forme indéterminée. Pour lever cette in\-dé\-ter\-mi\-na\-tion, il suffit de remarquer que $e^{2x} = \big( e^x\big)^2$, ce qui permet d'écrire $g (x)$ sous la forme $g (x) = e^x (2e^x - 1)$. On a alors la limite \dresultat{\lim_{x \to +\infty } g (x) = +\infty } puisque $\lim_{x \to +\infty } e^x = +\infty $. \itemalph L'existence d'une \tresultat{asymptote horizontale d'équation $y=0$} à la courbe de $g$ en $-\infty $ est prouvée par limite de $g$ en $-\infty $. \itemalph On a \dresultat{g' (x) = 4e^{2x} - e^x = e^x (4e^x - 1)}. \itemalph L'exponentielle étant toujours strictement positive, la dérivée $g'$ est du signe de $4e^x - 1$. Or $$ 4e^x - 1 \geq 0 \qquad \Longleftrightarrow \qquad e^x \geq {1\over 4} \qquad \Longleftrightarrow \qquad x \geq \ln \left( {1 \over 4}\right) = - 2\ln 2 $$ d'où le tableau des variations de $g$~: $$\vcenter{ \eightpoint\rm \def \hfq{\hfil \ } \offinterlineskip \halign{ % preamble &\hfq #\hfq \cr $x$& \vrule depth 5pt & $-\infty $&& $-2 \ln 2$&& $+\infty$% \cr \noalign{\hrule} $f' (x)$& \vrule height 10pt depth 3pt && $-$& $0$& $+$ \cr \noalign{\hrule} \bbuucenter{$f (x)$}& \vrule & \bbuup{$0$}& \bbrightddownarrow & \down{$-0, 125$}& \bbrightuuparrow & \bbuup{$+\infty $} \cr }} $$ où $g (-2\ln 2) = 2 e^{-4\ln 2} - e^{-2\ln 2} = 2 e^{\ln {1 \over 2^4}} - e^{\ln {1 \over 2^2}} = {2\over 16} - {1\over 4} = - {1\over 8}$ \itemnum On a $g (0) = 1$, donc l'intersection de la courbe de $g$ avec l'axe $Oy$ est le point \mresultat{A (0, 1)}. \item{} Rechercher l'intersection de la courbe représentative de la fonction $g$ avec l'axe $Ox$ revient à résoudre le système %%% %% pour la magnification 1000 %%% $$ %%% \cases{ %%% y = g (x) %%% \cr %%% y = 0 %%% \cr} %%% \quad \Leftrightarrow \quad %%% \cases{ %%% 0 = e^x (2e^x - 1) %%% \cr %%% y = 0 %%% \cr} %%% \quad \Leftrightarrow \quad %%% \cases{ %%% 0 = 2e^x - 1 %%% \cr %%% y = 0 %%% \cr} %%% \quad \Leftrightarrow \quad %%% \cases{ %%% 1/2 = e^x %%% \cr %%% y = 0 %%% \cr} %%% \quad \Leftrightarrow \quad %%% \cases{ %%% \ln (1/2) = x %%% \cr %%% y = 0 %%% \cr} %%% $$ %%% %% pour la magnification 1200 $$\displaylines{ \cases{ y = g (x) \cr y = 0 \cr} \qquad \Longleftrightarrow \qquad \cases{ 0 = e^x (2e^x - 1) \cr y = 0 \cr} \qquad \Longleftrightarrow \qquad \cases{ 0 = 2e^x - 1 \cr y = 0 \cr} \cr \qquad \Longleftrightarrow \qquad \cases{ 1/2 = e^x \cr y = 0 \cr} \qquad \Longleftrightarrow \qquad \cases{ \ln (1/2) = x \cr y = 0 \cr} \cr }$$ d'où l'unique point d'intersection \mresultat{B (-\ln 2, 0)}. \itemnum \def \epspath{% $HOME/tex_doc/lycee/database/term/sti/analyse/equadiff/} \epsfxsize = 120mm $$ \superboxepsillustrate{equ1_006.ps} $$ \itemnum Le nombre $g (0)$ étant positif, et $g$ étant croissante sur $[0, 1]$, la fonction $g$ est donc positive sur $[0, 1]$. L'aire cherchée est alors donnée, en unités d'aire, par le calcul $$ \int_0^1 g (x) \, dx = \int_0^1 2e^{2x} - e^x \, dx = \left[ e^{2x} - e^x \right]_0^1 = (e^2 - e) - (1 - 1) $$ d'où l'aire cherchée~: \dresultat{{\cal A} = e^2 - e} en unités d'aire. \fincorrige