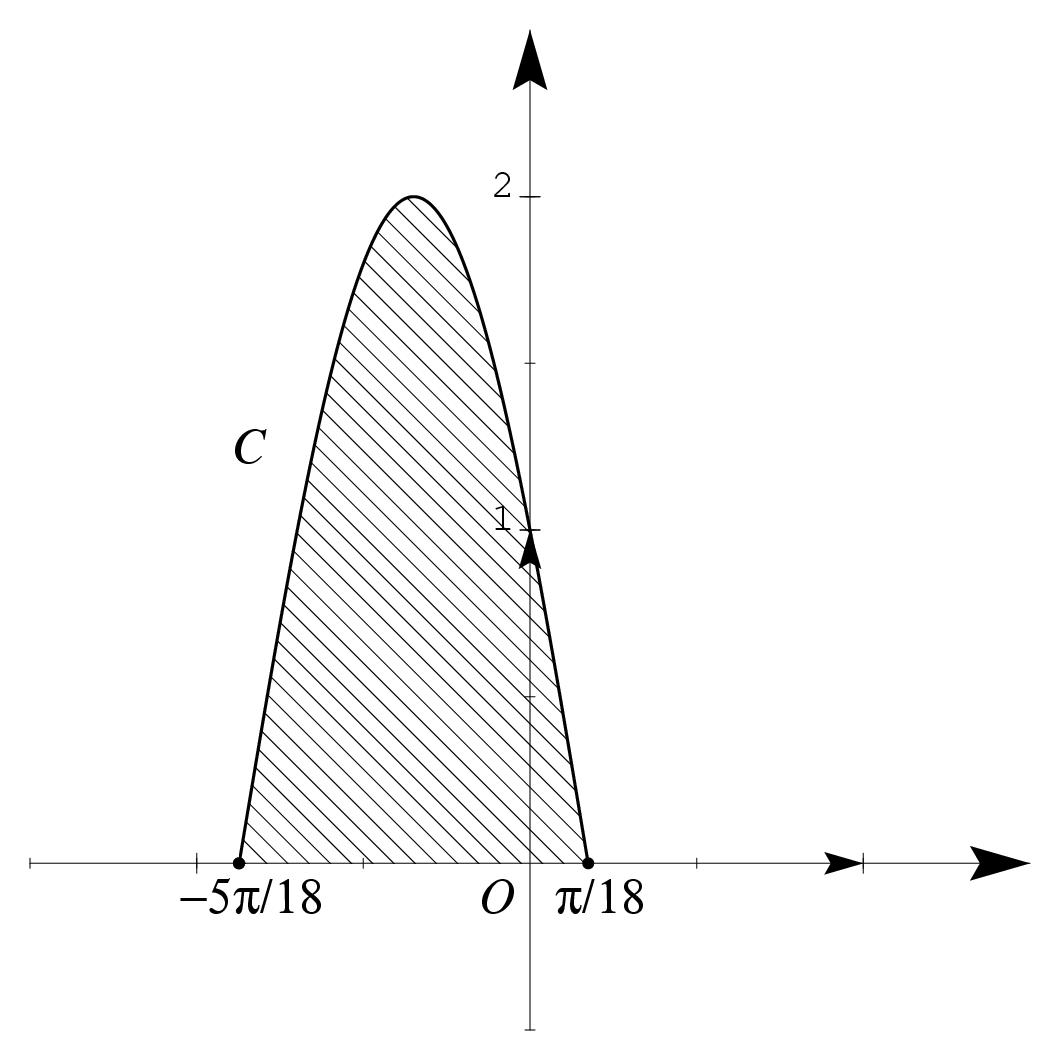
\exo{\'Equation différentielle d'ordre 2 -- Calcul de volume} \itemnum On considère l'équation différentielle $(E) : \quad y'' + 9y = 0$. \itemitemalph Résoudre l'équation $(E)$. \itemitemalph Déterminer la solution particulière $f$ de $(E)$ vérifiant $$ f \Big( {\pi \over2} \Big) = \sqrt3 \qquad {\rm et} \qquad f' \Big( {\pi \over2} \Big) = 3. $$ \itemitemalphnum Montrer que l'on peut écrire $f (x)$ sous la forme $$ f (x) = 2 \cos \Big( 3x + {\pi \over3}\Big) $$ \itemitemalph Résoudre dans l'intervalle $[-\pi/3, \pi/3]$ l'équation $f (x) = 0$. \itemnum On munit l'espace d'un repère orthonormé $(O, \vec \imath, \vec \jmath, \vec k\,)$ (unité graphique~: 3~cm). \def \epspath{% $HOME/tex_doc/lycee/database/term/sti/analyse/equadiff/} \epsfxsize = 70mm $$ \superboxepsillustrate{equ2_003.ps} $$ \item{} On appelle $C$ la courbe représentative dans le repère $(O, \vec \imath, \vec \jmath\,)$ de la fonction $g$ définie sur $[-5\pi / 18, \pi/18]$ par $$ g (x) = 2 \cos \Big( 3x + {\pi \over3}\Big) $$ Calculer le volume $V$ du solide engendré par la rotation autour de l'axe $(O, \vec \imath\,)$ de la partie du plan délimité par l' axe $(O, \vec \imath\,)$ et $C$. On exprimera le résultat en $\cm^3$. \finexo \corrige{} \itemalphnum On a $y'' + 9y = 0$ si et seulement si \mresultat{y = A \cos (3x) + B \sin (3x)} où $A$ et $B$ sont des réels quelconques. On en déduit en particulier que si $y$ est une solution de $(E)$, alors \mresultat{y' (x) = -3A \sin (3x) + 3B \sin (3x)}. \itemalph Si $f$ est une solution de $(E)$ vérifiant les conditions initiales imposées, alors $$ \cases{ f (\pi/2) = \sqrt3 \cr f' (\pi/2) = 3 \cr} \qquad \Longrightarrow \qquad \dresultat{\cases{ B = -\sqrt3 \cr A = 1 \cr}} \qquad {\rm d'où} \qquad \dresultat{f (x) = \cos 3x - \sqrt3 \sin 3x} $$ \itemalph En développant $\cos (3x + \pi/3)$ avec la formule $\cos (a+b) = \cos a \cos b - \sin a \sin b$, on obtient $$ 2 \cos \Big( 3x + {\pi \over3}\Big) = 2 \Big( \cos 3x \cos {\pi \over3} - \sin 3x \sin {\pi \over3}\Big) = \cos 3x - \sqrt3 \sin 3x \qquad {\rm soit} \qquad \dresultat{f (x) = 2 \cos \Big( 3x + {\pi \over3}\Big)} $$ \itemalph {\bf 1ére méthode~:} Si $x \in I = [-\pi/3, \pi/3]$, alors $3x \in [-\pi, \pi]$ et $(3x + \pi/3) \in [-2\pi/3, 4\pi/3]$. Résoudre l'équation $f (x) = 0$ pour $x \in [-\pi/3, \pi/3]$ revient donc à résoudre l'équation~: $$ \cos X = 0 \qquad {\rm pour} \quad X \in \left[ -{2\pi \over3}, {\pi \over3}\right] $$ équation on l'on a bien sûr posé $X = 3x + \pi/3$. Un simple dessin nous montre que les seules solutions pour $X$, dans l'intervalle considéré, sont les valeurs $X = \pi/2$ et $X = -\pi/2$. D'où la résolution de l'équation pour $x \in I = [-\pi/3, \pi/3]$~: $$ f (x) = 0 \quad \Longleftrightarrow \quad \cases{ 3x + \pi/3 = - \pi/2 \cr \quad {\rm ou} \cr 3x + \pi/3 = \pi/2 \cr} \quad \Longleftrightarrow \quad \cases{ 3x = - 5\pi/6 \cr \quad {\rm ou} \cr 3x = \pi/6 \cr} \quad \Longleftrightarrow \quad \dresultat{\cases{ x = - 5\pi/18 \cr \quad {\rm ou} \cr x = \pi/18 \cr}} $$ \item{} {\bf 2ème méthode~:} (sans réfléchir) On a, si $k$ désigne un entier relatif quelconque, $f (x) = 0$ si et seulement si $$ \cases{ 3x + \pi/3 = - \pi/2 + 2k\pi \cr \quad {\rm ou} \cr 3x + \pi/3 = \pi/2 + 2k\pi \cr} %\quad k \in \zset \quad \Leftrightarrow \quad \cases{ 3x = - 5\pi/6 + 2k\pi \cr \quad {\rm ou} \cr 3x = \pi/6 + 2k\pi \cr} \quad \Leftrightarrow \quad \cases{ x = - 5\pi/18 + 2k\pi/3 \cr \quad {\rm ou} \cr x = \pi/18 + 2k\pi/3 \cr} $$ En essayant les différentes valeurs possibles pour l'entier $k$, on s'aperçoit que l'équation $f (x) = 0$ n'admet que deux solutions dans l'intervalle $I$ considéré~: \mresultat{x = - 5\pi/18} et \mresultat{x = \pi/18}. \itemnum L'unité graphique étant de 3~cm, le volume $V$ engendré est donné par le calcul $$ V = 3^3 \int_{-5\pi/18}^{\pi/18} \pi g^2 (x) \, dx \cm^3. $$ En posant $x_1 = -5\pi/18$ et $x_2 = \pi/18$, il vient $$\eqalign{ V &= 27 \pi \int_{x_1}^{x_2} g^2 (x)\, dx = 108 \pi \int_{x_1}^{x_2} \cos^2 \Big( 3x + {\pi \over3}\Big) \, dx = {108 \pi \over2} \int_{x_1}^{x_2} 1 + \cos \Big( 6x + {2\pi \over3}\Big) \, dx \cr &= 54 \pi \left[ x + {1\over6} \sin \Big( 6x + {2\pi \over3}\Big)\right]_{x_1}^{x_2} \qquad {\rm soit} \qquad \mresultat{V = 18 \pi^2 \cm^3}. \cr }$$ \fincorrige