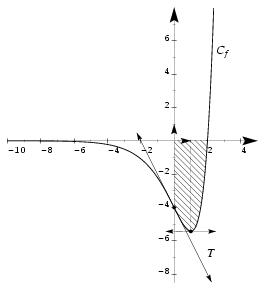
\exo {Une étude facile, {\sl bac F6}, {\sl 1993}} On considère la fonction numérique de la variable $x$ définie sur $\rset $ par $$ f (x) = (2x-4) e^x. $$ On note $C_f$ la courbe représentative de la fonction $f$ dans le plan muni d'un repère orthonormal $(O, \vec \imath , \vec \jmath )$ d'unité graphique 1~cm. \itemitemalphnum Calculer la limite de $f (x)$ quand $x$ tend vers $+\infty $. \itemitemalph Calculer la limite de $f (x)$ quand $x$ tend vers $-\infty $. On pourra écrire $f (x)$ sous la forme $$ f (x) = 2x e^x - 4e^x. $$ \itemitemalphnum Montrer que la dérivée $f'$ de $f$ peut s'écrire $$ f' (x) = 2 (x-1) e^x. $$ \itemitemalph \' Etudier le signe de $f' (x)$ pour $x$ réel. En déduire le tableau de variation de la fonction $f$. \itemnum Déterminer une équation de la tangente $T$ à la courbe $C_f$ en son point d'abscisse nulle. \itemnum Tracer la tangente $T$ et la courbe $C_f$. \itemnum Soit $F$ la fonction numérique de variable réelle $x$ définie sur $\rset $ par $$ F (x) = (ax+b) e^x \qquad {\rm où} \qquad \hbox {$a$ et $b$ sont des réels.} $$ \itemitemalph Calculer $F' (x)$. \itemitemalph Déterminer $a$ et $b$ pour que $F (x)$ soit une primitive de $f$ sur $\rset $. \itemnum Calculer la valeur exacte exprimée en cm$^2$ de l'aire de l'ensemble des points $M$ du plan de coordonnées $(x, y)$ vérifiant $$ \cases { 0 \leq x \leq 2 \cr f (x) \leq y \leq 0 \cr } $$ En donner une valeur approchée à $10^{-2}$ près. \finexo \corrige {} \itemalphnum On a \dresultat {\lim _{x\to +\infty }f (x) = +\infty } puisque $$ f (x) = (2x-4) e^x \qquad {\rm avec} \qquad \cases { \displaystyle \lim _{x\to +\infty } (2x-4) = +\infty \cr \displaystyle \lim _{x\to +\infty } e^x = +\infty \cr } $$ \itemalph Et on a \dresultat {\lim _{x\to -\infty }f (x) = 0} puisque $$ f (x) = 2xe^x -4e^x \qquad {\rm avec} \qquad \cases { \displaystyle \lim _{x\to -\infty } xe^x = 0& (formulaire) \cr \displaystyle \lim _{x\to -\infty } e^x = 0 \cr } $$ On en déduit que la courbe de la fonction $f$ admet \tresultat {l'axe $Ox$ comme asymptote horizontale}. \itemnum On trouve $f' (x) = 2e^x + (2x-4)e^x$, soit \dresultat {f'(x) = 2 (x-1) e^x}. Comme $e^x$ est toujours strictement positif, cette dérivée est du signe de $x-1$ et on a immédiatement le tableau de variation suivant~: $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& -\infty && 1&& +\infty \cr \noalign {\hrule height 1pt } f' (x)&& &-& 0& + \cr \noalign {\hrule height 1pt} \buucenter {$f (x)$}&& \buup {$0$}& \brightddownarrow & \down{$-2e \approx -5,436$}& \brightuuparrow & \buup {$+\infty $} \cr }} }$$ \itemnum On a $f (0) = -4$ et $f' (0) = -2$. En utilisant la formule $y = f' (a) (x-a) + f (a)$, il vient \dresultat {T~: y = -2x-4} \def \epspath {% $HOME/tex_doc/lycee/database/term/sti/analyse/exp/} \epsfysize = 90mm \itemnum $$ \superboxepsillustrate {etud_003.ps} $$ \itemalphnum On trouve $F' (x) = ae^x + (ax+b)e^x$, soit \dresultat {F' (x) = (ax + a+b)e^x}. \itemalph Pour que $F$ soit une primitive de $f$, on doit avoir $F' (x) = f (x)$, soit $(ax + a+b) = (2x-4)$. D'où le système d'équation $$ \cases { a = 2 \cr a+b = -4 \cr } \qquad \Longleftrightarrow \qquad (a, b) = (2, -6) $$ La fonction $F$ définie par \dresultat {F (x) = (2x-6) e^x} est donc la primitive de $f$ cherchée. \itemnum D'après la définition donnée du domaine plan, on voit que $f (x)$ est négatif pour $x$ dans l'intervalle $[0, 2]$. Comme l'unité d'aire est de 1~cm$^2$, l'aire $\cal A$ est donnée par le calcul $$ {\cal A} = - \int _0^2 f (x) \, dx = \int _2^0 f (x) \, dx = \Big[ F (x) \Big] _2^0 = F (0) - F (2) = -6 + 2e^2. $$ On a donc \dresultat {{\cal A} = 2e^2 - 6\cm ^2 \approx 8, 78 \cm ^2}. \fincorrige