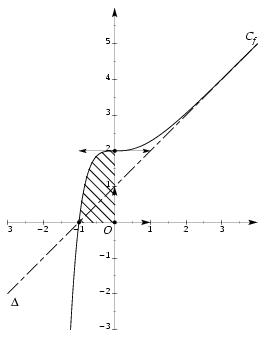
\exo {Un problème \og standard\fg \ ({\sl Bac gm, septembre 96})} \let \partie \centerpartie \partie {A} On considère la fonction $g$ de la variable $x$, définie sur $\rset $ par~: $$ g (x) = e^{2x} - 2x -1. $$ Le but de cette première partie est l'étude, pour tout réel $x$, du signe de $g (x)$. \itemnum Résoudre dans $\rset $ l'inéquation d'inconnue $x$~: \quad $e^{2x} - 1 \geq 0$. \itemitemalphnum \' Etudier le sens de variation de la fonction $g$ (l'étude des limites n'est pas demandée). \itemitemalph En déduire que, pour tout $x$ de $\rset $, $g (x) \geq 0$. \partie {B} L'objet de cette deuxième partie est l'étude de la fonction $f$ de la variable $x$, définie sur $\rset $ par~: $$ f (x) = (x+1) e^{-2x} + x + 1. $$ On note $C_f$ la courbe représentative de la fonction $f$ dans le plan rapporté à un repère orthonormé $(O, \vec \imath , \vec \jmath )$ (unité~: 2~cm). L'axe des abscisses est noté $Ox$, celui des ordonnées est noté $Oy$. \itemnum Calculer la limite de $f (x)$ quand $x$ tend vers $-\infty $. \itemitemalphnum Vérifier que, pour tout réel $x$~: $$ f (x) = (xe^{-x})e^{-x} + e^{-2x} + x + 1. $$ \itemitemalph En déduire la limite de $f (x)$ quand $x$ tend vers $+\infty $. \itemitemalph Montrer que la droite $\Delta $, d'équation $y = x+1$ , est asymptote à $C_f$ quand $x$ tend vers $+\infty $. \itemitemalph Montrer que si $x\geq -1$, alors $f (x) \geq x+1$. En déduire la position de la courbe $C_f$ par rapport à $\Delta $ lorsque $x \geq -1$. \itemitemalphnum Montrer que la fonction dérivée $f'$ de $f$ est définie, pour tout $x$ réel, par~: $$ f' (x) = e^{-2x} g (x). $$ \itemitemalph \' Etudier pour tout $x$ réel le signe de $f' (x)$ et établir le tableau de variation de $f$. \itemitemalphnum Reproduire et compléter le tableau suivant (donner pour $f (x)$ des valeurs arrondies à $10^{-2}$). $$\vcenter {\offinterlineskip \def \cc#1{% \hbox to 10mm {\hfill #1\hfill }} \halign { % preamble #\tv && \cc {$#$}& #\tv \cr \noalign {\hrule } & x&& -2&& -1, 5&& -1, 3&& -1, 1&& -1&& -0, 5&& 0&& 0, 5&& 1&& 2&& 3&& 4& \cr \noalign {\hrule } & f (x)&& && && && && && && && && && && && & \cr \noalign {\hrule } }} $$ \itemitemalph Tracer la droite $\Delta $ et la courbe $C_f$ dans le plan rapporté au repère $(O, \vec \imath , \vec \jmath )$. \partie {C} On considère les fonctions $H$ et $h$, respectivement définie sur $\rset $ par~: $$ H (x) = \left( - {1\over 2} x - {3\over 4}\right) e^{-2x} \qquad {\rm et} \qquad h (x) = (x+1)e^{-2x}. $$ \itemnum Vérifier que $H$ est une primitive de $h$ sur $\rset $. \itemnum En déduire une primitive $F$ de $f$ sur $\rset $. \itemnum Calculer l'aire de la partie du plan limité par la courbe $C_f$, l'axe des abscisses et les droites d'équations $x=-1$ et $x=0$. (On donnera la valeur exacte exprimée en cm$^2$). \finexo \corrige \let \partie \llappartie \partie {A} % \num \ On a $$ e^{2x} - 1 \geq 0 \quad \Longleftrightarrow \quad \ln \left( e^{2x} \right) \geq \ln (1) \quad \Longleftrightarrow \quad 2x \geq 0 \quad \Longleftrightarrow \quad \dresultat {x \geq 0} $$ \alphnum \ On a $g' (x) = 2 e^{2x} - 2$, soit \dresultat {g' (x) = 2 \big( e^{2x} - 1\big)}. Donc $g'$ est du signe de $e^{2x} - 1$, et la question {\bf 1.} nous prouve que \tresultat {$g' (x)$ est positif si $x$ est positif, négatif sinon}. D'où le tableau de variations de $g$~: $$\dresultat {\vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& -\infty && 0&& +\infty \cr \noalign {\hrule height 1pt } g' (x)&& &-& 0& + \cr \noalign {\hrule height 1pt} \buucenter {$g (x)$}&& & \brightddownarrow & \down{$0$}& \brightuuparrow & \buup {\phantom {1}} \cr }}} $$ \alph \ Comme le minimum de $g$ est $g (0) = 0$, on en déduit que \tresultat {$g (x) \geq 0$ pour tout $x$ réel}. \partie {B} % \num \ On a $$ \lim _{x \to -\infty } f (x) = \lim _{x \to -\infty } \downto {(x+1)}{-\infty } \downto {\phantom {(}e^{-2x}}{+\infty } + \downto {\phantom {(}x}{-\infty } + 1 \qquad {\rm soit}\qquad \dresultat {\lim _{x \to -\infty } f (x) = -\infty } $$ \alphnum \ On vérifie facilement l'égalité proposée en utilisant le fait que $e^{-x} \times e^{-x} = e^{-2x}$. \alph \ Il vient alors~: $$ \lim _{x \to +\infty } f (x) = \lim _{x \to +\infty } (xe^{-x})e^{-x} + e^{-2x} + x + 1 \qquad {\rm soit}\qquad \dresultat {\lim _{x \to +\infty } f (x) = +\infty } $$ \bgroup \everymath = {\displaystyle } puisque $ \lim _{x \to +\infty }xe^{-x} = 0$ d'après le cours, et que $\lim _{x \to +\infty } e^{-x} = \lim _{x \to +\infty } e^{-2x} = 0$ \egroup \alph \ Pour montrer que $\Delta $ est asymptote à $C_f$, on calcule la limite de la différence entre $f (x)$ et $x+1$. Il vient alors $$ \lim _{x \to +\infty } f (x) - (x+1) = \lim _{x \to +\infty }(x+1)e^{-x} = \lim _{x \to +\infty }xe^{-x} + e^{-x} = 0 $$ pour les mêmes raisons qu'à la question précédente. Donc \tresultat {$\Delta $ asymptote à $C_f$ en $+\infty $}. \alph \ On sait que $$ f (x) - (x+1) = (x+1) e^{-2x}. $$ Et comme l'exponentielle est toujours positive, cette différence est du signe de $x+1$, c'est à dire négative pour $x\leq -1$ et positive pour $x\geq -1$. Autrement dit \tresultat {$f (x) \geq x+1$ pour $x\geq -1$}, et \tresultat {$f (x) \leq x+1$ sinon}. En conclusion, \tresultat {$C_f$ est au-dessus de $\Delta $ pour $x\geq -1$ et en-dessous sinon}. \alphnum \ On a $f (x) = (x+1) e^{-2x} + x + 1$, et donc $$ f' (x) = e^{-2x} - 2 (x+1)e^{-2x} + 1 \qquad {\rm soit} \qquad \dresultat {f' (x) = - e^{-2x} - 2 x e^{-2x} + 1} $$ Or $$ e^{-2x} g (x) = e^{-2x} \left( e^{2x} - 2x -1 \right) = e^{-2x+2x} -2x e^{-2x} - e^{-2x} = 1 -2x e^{-2x} - e^{-2x} $$ donc on a bien \dresultat {f' (x) = e^{-2x} g (x)}. \alph \ L'exponentielle étant toujours positive, on a donc $f'$ qui est du signe de $g$, et on utilise alors la partie {\bf A.} pour établir le tableau de variations de $f$~: $$\dresultat {\vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& -\infty && 0&& +\infty \cr \noalign {\hrule height 1pt } f' (x)&& &+& 0& + \cr \noalign {\hrule height 1pt} \buucenter {$f (x)$}&& \down {$-\infty $}& \brightuparrow & \buucenter {$2$}& \bup {\brightuparrow }& \buup {$+\infty $} \cr }}} $$ \alphnum \ On trouve $$\vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{% \hbox to 12mm {\hfill #1\hfill }} \halign { % preamble #\tv && \cc {$#$}& #\tv \cr \noalign {\hrule } & x&& -2&& -1, 5&& -1, 3&& -1, 1&& -1&& -0, 5&& 0&& 0, 5&& 1&& 2&& 3&& 4& \cr \noalign {\hrule } & f (x)&& -55, 60&& -10, 54&& -4, 34&& -1&& 0&& 1, 86&& 2&& 2, 05&& 2, 27&& 3, 05&& 4, 01&& 5& \cr \noalign {\hrule } }} $$ \def \epspath {% $HOME/tex_doc/lycee/database/term/sti/analyse/exp/} \epsfxsize 100mm \alph $$ \superboxepsillustrate {pbm_006.ps} $$ \partie {C} % \num \ La fonction $H$ est un produit de fonctions. On utilise la formule $(uv)' = u'v+uv'$ pour obtenir $$ H' (x) = - {1\over 2} e^{-2x} - 2 \left( - {1\over 2} x - {3\over 4}\right) e^{-2x} = - {1\over 2} e^{-2x} + x e^{-2x} + {3\over 2} e^{-2x} $$ soit \mresultat {H' (x) = h (x)}. On a bien le fait que \tresultat {$H$ est une primitive de $h$ sur $\rset $}. \num \ Et comme $f (x) = h (x) + x + 1$, on en déduit qu'une primitive de la fonction $f$ est la fonction $F$ définie par $$ \dresultat {F (x) = H (x) + {x^2\over 2} + x} $$ \num \ L'unité d'aire étant de $2\times 2 = 4\cm ^2$, l'aire demandée est donnée par le calcul $$\eqalign { {\cal A} &= 4\times \int _{-1}^0 f (x)\, dx = 4\times \big[ F (x)\big] _{-1}^0 = 4 (F (0) - F (-1)) = 4 \left( H (0) - H (-1) - {1\over 2} + 1\right) \cr &= 4 \left( - {3\over 4} + {1\over 4}e^2 + {1\over 2} \right) \qquad {\rm soit} \qquad \dresultat {{\cal A}= (e^2 - 1) \cm ^2 \approx 6, 39 \cm ^2} \cr }$$ \fincorrige