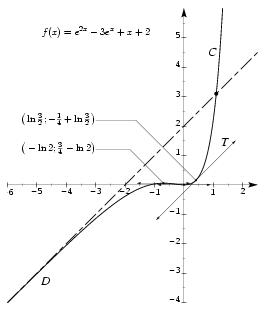
\exo {Un problème avec de l'exponentielle, {\sl bac stl cl, 2001}} Soit $f$ la fonction définie sur $\rset $ par $$ f (x) = e^{2x} - 3e^x + x + 2 $$ et $\cal C$ sa courbe représentative dans le plan muni d'un repère orthonormalo $(O, \vec \imath , \vec \jmath )$ d'unité graphique $4~\cm$. \itemitemalphnum Déterminer la limite de $f (x)$ quand $x$ tend vers $+\infty $. \itemitemalph Démontrer que la droite $D$ d'équation $y = x+2$ est asymptote à $\cal C$. \itemitemalph \' Etudier les positions relatives de la courbe $\cal C$ et de la droite $D$. \itemnum Vérifier que pour tout réel $x$~: $$ f (x) = e^x \left( e^x - 3 + {x\over e^x} + {2 \over e^x}\right). $$ En déduire la limite de $f (x)$ quand $x$ tend vers $+\infty $. \itemitemalphnum Calculer $f' (x)$. \itemitemalph Vérifier que $f' (x) = (2e^x - 1) (e^x -1)$. \itemitem {} Résoudre dans $\rset $ l'équation $f' (x) = 0$ puis déterminer le signe de $f' (x)$. \itemitemalph Dreseer le tableau de variations de $f$. \itemitemalphnum Déterminer une équation de la tangente $T$ à la courbe $\cal C$ en son point d'abscisse $\ln (2/3)$. \itemitem {} Que peut-on dire des droites $T$ et $D$~? \itemitemalph Tracer, dans le repère $(O, \vec \imath , \vec \jmath \,)$, les droites $D$, $T$ et la courbe $\cal C$. \itemnum Calculer l'aire, en $\cm ^2$, de la partie du plan limitée par la courbe $\cal C$, la droite $D$ et les droites d'équation $x=0$ et $x=\ln 3$. \finexo \corrige {} \itemalphnum Il vient $$ \dresultat {\lim _{x\to -\infty } f (x) = -\infty } \qquad {\rm puisque} \qquad f (x) = e^{2x} - 3e^x + x + 2 \qquad {\rm avec} \qquad \cases { \lim _{x\to -\infty } e^{2x} = 0 \cr \lim _{x\to -\infty } -3e^{x} = 0 \cr \lim _{x\to -\infty } x+2 = -\infty \cr } $$ \itemalph On a $$ f (x) - (x+2) = e^{2x} - 3e^x \qquad {\rm donc} \qquad \lim _{x\to -\infty } f (x) - (x+2) = 0 $$ d'après {\bf 1.}{\sl a\/}). Ce qui prouve que la droite \tresultat {$y = x+2$ est asymptote à la courbe $\cal C$ en $-\infty $}. \itemalph \' Etudier les positions relatives de $\cal C$ et de $D$ revient à étudier le signe de la différence $f (x) - (x+2)$. Il vient alors $$\displaylines { f (x) - (x+2) = e^{2x} - 3e^x = e^x \big( e^x - 3\big) \cr {\rm or} \qquad e^x - 3 \geq 0 \quad \Longleftrightarrow \quad e^x \geq 3 \quad \Longleftrightarrow \quad x \geq \ln 3 \cr } $$ d'où le tableau de signes et la conclusion~: $$\dresultat { \vcenter {\halign {\offinterlineskip %% preamble \cc {$#$}& #\tv && \cc {#} \cr x&& $-\infty $&& $\ln 3$&& $+\infty$ \cr \noalign {\hrule height 1pt} e^x&&& $+$ & \tv & $+$ \cr \noalign {\hrule } e^x - 3&&& $-$ & $0$& $+$ \cr \noalign {\hrule height 1pt} f (x) - (x+2)&&& $-$ & $0$& $+$ \cr \noalign {\hrule height 1pt} \hbox {positions relatives}&&& $\cal C$ au dessous de $D$& \tv & $\cal C$ au dessus de $D$% \cr }} } $$ \itemnum En développant l'expression proposée, il vient $$ e^x \left( e^x - 3 + {x\over e^x} + {2 \over e^x}\right) = e^{x+x} - 3e^x + {xe^x\over e^x} + {2e^x \over e^x} e^{2x} - 3e^x + x + 2. $$ On a donc bien $$ \dresultat { f (x) = e^x \left( e^x - 3 + {x\over e^x} + {2 \over e^x}\right) } \qquad \hbox {d'où l'on déduit} \qquad \dresultat {\lim _{x\to +\infty } f (x) = +\infty } $$ puisque $$ \lim _{x\to +\infty } e^x = +\infty \qquad \lim _{x\to +\infty } e^x -3 = +\infty \qquad \lim _{x\to +\infty } {x\over e^x} = 0 \quad {\rm (formulaire)} \quad \qquad \lim _{x\to +\infty } {2\over e^x} = 0. $$ \itemalphnum En partant de l'écriture $f (x) = e^{2x} - 3e^x + x + 2$, on a immédiatement \dresultat {f' (x) = 2e^{2x} - 3e^x +1}. \itemalph \alph \ Et en développant l'expression proposée, il vient $$ (2e^x - 1) (e^x -1) = 2e^{2x} - e^x - 2e^x +1 = 2e^{2x} - 3e^x +1 \qquad {\rm soit} \qquad \dresultat {f' (x) = (2e^x - 1) (e^x -1)} $$ Comme on a $$\displaylines { 2e^x - 1 = 0 \quad \Longleftrightarrow \quad e^x = {1\over 2} \quad \Longleftrightarrow \quad x = \ln {1\over 2} = -\ln 2 \cr {\rm et} \qquad e^x - 1 = 0 \quad \Longleftrightarrow \quad e^x = 1 \quad \Longleftrightarrow \quad x = \ln 1 = 0 \cr } $$ on a le tableau récapitulatif suivant~: $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& -\infty && -\ln 2&& 0&& +\infty & \cr \noalign {\hrule height 1pt} e^x - 1&& & - & \tv & -& 0& +& & \cr \noalign {\hrule } 2e^x - 1&& & - & 0& +& \tv & +& & \cr \noalign {\hrule height 1pt} \buucenter {$f (x)$}&& \down {$-\infty $}& \brightuuparrow & \buup {${3\over 4} - \ln 2$}& \brightddownarrow & \down{$0$}& \brightuuparrow & \buup {$+\infty $} \cr }} }$$ où $$ \eqalign { f (-\ln 2) &= e^{-2\ln 2} -3e^{-\ln 2} - \ln 2 + 2 \cr &= e^{\ln 2^{-2}} -3e^{\ln 2^{-1}} - \ln 2 + 2 \cr &= {1\over 4} - {3\over 2}- \ln 2 + 2 = {3\over 4} - \ln 2 \approx 0, 057 \cr } $$ \itemalphnum On a $$ \vtop {\hsize = .45 \hsize $\displaystyle \eqalign { f \big( \ln (3/2)\big) &= e^{2\ln (3/2)} -3e^{\ln (3/2)} + \ln (3/2) + 2 \cr &= e^{\ln (9/4)} -3\times {3\over 2} + \ln (3/2) + 2 \cr &= {9\over 4} -{9\over 2} + \ln (3/2) + 2 \cr &= -{1\over 4} + \ln (3/2) \approx 0, 15 \cr } $} \tv \ \vtop {\hsize = .45 \hsize $\displaystyle \eqalign { f' \big( \ln (3/2)\big) &= 2e^{2\ln (3/2)} -3e^{\ln (3/2)} + 1 \cr &= 2e^{\ln (9/4)} -3\times {3\over 2} +1 \cr &= {9\over 2} - {9\over 2} + 1 \cr &= 1 \cr } $} $$ D'où l'équation de la tangente~: $$ T~: y = \Big(x-\ln {3\over 2}\Big) - {1\over 4} + \ln {3\over 2} \qquad {\rm soit} \qquad \dresultat { T~: y = x + {1\over 4} } $$ Le coefficient directeur de la droite $T$ est $f' (\ln (3/2)) = 1$, autrement dit les droites $T$ et $D$ ont le même coefficient directeur, ce qui permet d'affirmer que \tresultat {$T$ et $D$ sont parallèles}. \itemalph \def \epspath {% $HOME/tex_doc/lycee/database/term/sti/analyse/exp/} $$ \superboxepsillustrate {pbm_009.ps} $$ \itemnum Comme $C$ est au-dessous de $D$ sur l'intervalle $[0; \ln 3]$ considéré, et comme l'unité d'aire est de $4\cm \times 4\cm = 16\cm ^2$, l'aire cherchée est $$ \eqalign { {\cal A} &= 16 \times \int _0^{\ln 3} (x+2) - f (x) \, dx \cr &= 16 \times \int _0^{\ln 3} -e^{2x} + 3e^x \, dx \cr &= 16 \times \Big[ -{1\over 2}e^{2x} + 3e^x \Big] _0^{\ln 3} \cr &= 16 \times \Big( \Big( -{1\over 2}e^{2\ln 3} + 3e^{\ln 3} \Big) - \Big( -{1\over 2} + 3\Big) \Big) \cr &= 16 \times \Big( \Big( -{9\over 2}+9 \Big) - {5\over 2} \Big) \qquad {\rm soit} \qquad \dresultat {{\cal A} = 32\cm ^2} \cr } $$ \fincorrige