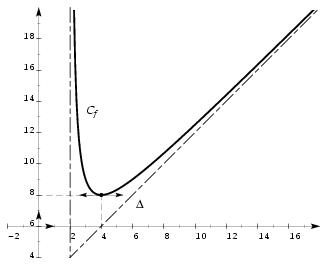
\exo{\'Etude d'une fonction rationnelle. ({\sl d'après Bac $F_1$, 1991})} On considère $f$, la fonction numérique de la variable réelle $x$ définie sur l'intervalle $]2, +\infty[$ par $$ f (x) = x + 2 + {4 \over x-2}. $$ Soit $C_f$ sa courbe représentative dans un repère orthonormal d'unité 1~cm (ou 1~grand carreau). \itemnum \'Etudier la limite de $f$ en $+\infty$. \itemitemalphnum Montrer que la courbe $C_f$ admet la droite $\Delta$ d'équation $y = x + 2$ pour asymptote. \itemitemalph \'Etudier la position de $C_f$ par rapport à $\Delta$. \itemitemalphnum \'Etudier la limite de $f$ en 2. \itemitemalph En déduire l'équation d'une asymptote à la courbe $C_f$. \itemitemalphnum Calculer la dérivée $f'$ de $f$ et montrer qu'elle peut s'écrire sous la forme $$ f' (x) = {x^2 -4x\over (x-2)^2} $$ \itemitemalph \' Etudier le signe de $f' (x)$ pour $x$ appartenant à l'intervalle $]2, +\infty[ $. En déduire le tableau de variations de la fonction $f$. \itemnum Représenter la courbe $C_f$ dans le repère donné. \itemnum Déterminer une équation de $T$, la tangente à la courbe $C_f$ au point d'abscisse $3$. %% \itemitemalphnum Déterminer, en $\cm ^2$, l'aire du domaine plan limité par la %% courbe $C_f$, la droite $\Delta $ et les droites $x = 4$ et $x = 10$. %% %% \itemitemalph Hachurer ce domaine sur votre graphique. %% %% \bigskip %% \centerline{\bf Voir la suite dans l'Anabac Nathan non corrigé, 1998, %% Stt-Sti, p~173} \finexo \corrige{} \itemnum On a bien sûr \dresultat{\lim_{x \rightarrow +\infty} f (x) = +\infty} puisque $$ f (x) = x + 2 + {4\over x-2} \qquad {\rm avec} \qquad \cases { \displaystyle{ \lim_{x \rightarrow +\infty} {4\over x-2} = 0 } \cr \cr \displaystyle{ \lim_{x \rightarrow +\infty} x+2 = +\infty } \cr } $$ \itemalphnum On a $\displaystyle{ \lim_{x \rightarrow +\infty} \left[ f (x) - (x+2)\right] = \lim_{x \rightarrow +\infty} {4\over x-2} = 0 }$. Donc on a bien \tresultat{$\Delta$ asymptote à $C_f$ en $+\infty$}. \itemalph De plus, la différence $f (x) - (x+2)$ est égale à $4/ (x-2)$ qui est du signe de $(x-2)$. On en déduit, puisque $x > 2$, que $(x-2)$ est toujours positif sur l'intervalle, et donc que \tresultat{$C_f$ est toujours au dessus de $\Delta $} sur l'intervalle $]2, +\infty [$. \itemalphnum Et on a \dresultat{\lim_{x \rightarrow 2^+} f (x) = + \infty } puisque $$ f (x) = x + 2 + {4\over x-2} \qquad {\rm avec} \qquad \cases { \displaystyle{ \lim_{x \rightarrow 2^+} x-2 = 0^+ } \cr \cr \displaystyle{ \lim_{x \rightarrow 2^+} {4\over x-2} = +\infty } \cr \cr \displaystyle{ \lim_{x \rightarrow 2} x+2 = 4 } \cr } $$ \itemalph On en déduit immédiatement que \tresultat{la droite $x=2$ est asymptote verticale à $C_f$} \itemnum On a $$ f' (x) = 1 - {4 \over (x-2)^2} = {x^2 -4x + 4 - 4 \over (x-2)^2} \qquad {\rm soit} \qquad \dresultat{f' (x) = {x (x - 4) \over (x-2)^2}} $$ qui est du signe de $x (x - 4)$ puisque $(x-2)^2$ est toujours positif, et donc du signe de $(x-4)$ puisque $x>2$ par définition de $f$. D'où le tableau de signe de $f'$, suivi du tableau de variations de $f$~: $$\dresultat{\vbox{ \eightpoint\rm \def \hfq{\hfil \ } \offinterlineskip \halign{ % preamble &\hfq #\hfq \cr $x$& \tv height 7pt& $2$&& $4$&& $+\infty$% \cr \noalign{\hrule} $x-4$& \vrule height 10pt depth 3pt && $-$& $0$& $+$% \cr \noalign{\hrule} $f' (x)$& \vrule height 10pt depth 3pt && $-$& $0$& $+$% \cr \noalign{\hrule} \bbuucenter{$f (x)$}& \vrule& \bbuup{$+\infty$}\hfill& \bbrightddownarrow & \down{$8$}& \bbrightuuparrow & \bbuup{$+\infty$}% \cr }} }$$ \def \epspath{% $HOME/tex_doc/lycee/database/term/sti/analyse/fonctions/} \epsfxsize = 110mm $$ \superboxepsillustrate{frct_008.ps} $$ \itemnum On a $f (3) = 9$ et $f' (3) = -3$, d'où l'équation de $T$~: $$ y = -3 (x-3) + 9 \qquad {\rm soit} \qquad \dresultat {T~: y = -3x + 18 } $$ \fincorrige{}