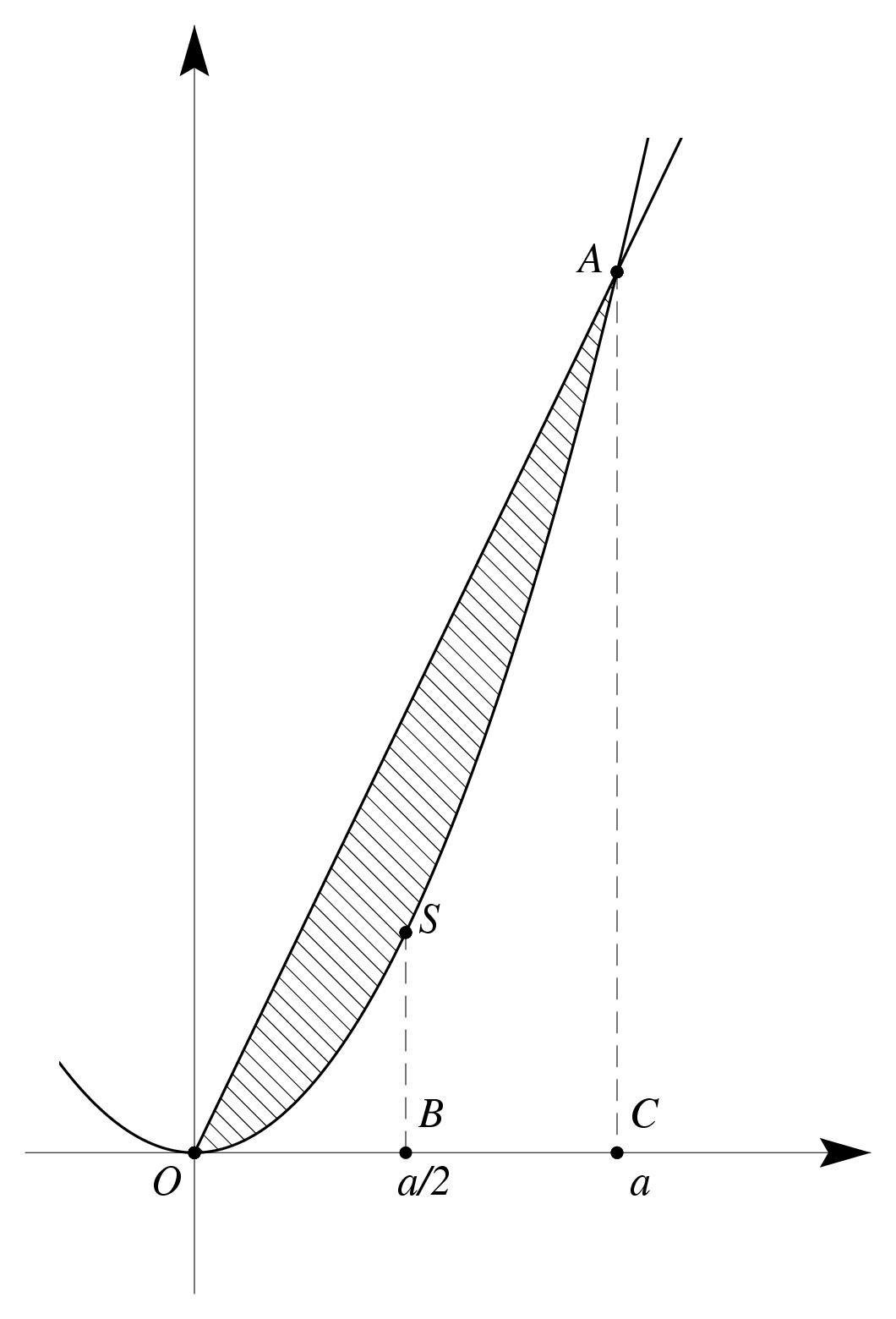
%% format (plain.tex + fichiers de macro) OU (jpv.tex) %% fichiers de macro basejpv.tex %% sujet %% date 05-12-97 %% auteur jp vignault \exo{Intersection parabole -- droite variable, calcul d'aire} \bigskip \def \epspath{% $HOME/tex_doc/lycee/database/term/sti/analyse/integr/} \epsfxsize = 52mm \rightsuperboxepsillustrate{aire_003.ps}{-15} On considère $\cal P$ la parabole d'équation $y=x^2$ dans un plan rapporté à un repère orthonormé $(O,\vec \imath, \vec \jmath)$. Soit $a$ un réel strictement positif. On note $A$ le point de $\cal P$ d'abscisse $a$, et $S$ le point de $\cal P$ d'abscisse ${a \over 2}$. On note $\cal A$ l'aire de $\Sigma_A$, ensemble des points du plan limité par l'arc de parabole $\widehat{OSA}$ et le segment $[OA]$. (Sur la figure, on a hachuré $\Sigma_A$.) On note $\cal B$ l'aire du triangle $OSA$. Le but de l'exercice est de montrer que le rapport $\cal A \over \cal B$ est constant lorsque le réel $a$ varie dans $]0 ; +\infty[$. \num\ Quelle est l'équation de la droite $(OA)$~? \num\ Soit $C$ la projection orthogonale de $A$ sur l'axe $(x'x)$, et $B$ la projection orthogonale de $S$ sur $(x'x)$. \alph\ Quelle est, en fonction de $a$, l'aire du triangle $OCA$~? \alph\ Quelle est, en fonction de $a$, l'aire du triangle $OBS$~? \alph\ Quelle est, en fonction de $a$, l'aire du trapère $BCAS$~? \alph\ En déduire $\cal B$ en fonction de $a$. \num\ Calculer l'aire $\cal A$ en fonction de $a$. \num\ Montrer la propriété cherchée. \finexo \endinput %% ============== svegarde ================== \exo{Intersection de deux paraboles, calcul d'aire} \setbox \tmpbox = \vbox{% \advance \hsize by -60truemm % On considère $\cal P$ la parabole d'équation $y=x^2$ dans un plan rapporté à un repère orthonormé $(O,\vec \imath, \vec \jmath)$. Soit $a$ un réel strictement positif. On note $A$ le point de $\cal P$ d'abscisse $a$, et $S$ le point de $\cal P$ d'abscisse ${a \over 2}$. On note $\cal A$ l'aire de $\Sigma_A$, ensemble des points du plan limité par l'arc de parabole $\widehat{OSA}$ et le segment $[OA]$. (Sur la figure, on a hachuré $\Sigma_A$.) On note $\cal B$ l'aire du triangle $OSA$. Le but de l'exercice est de montrer que le rapport $\cal A \over \cal B$ est constant lorsque le réel $a$ varie dans $]0 ; +\infty[$. \itemnum Quelle est l'équation de la droite $(OA)$~? \itemnum Soit $C$ la projection orthogonale de $A$ sur l'axe $(x'x)$, et $B$ la projection orthogonale de $S$ sur $(x'x)$. \alph\ Quelle est, en fonction de $a$, l'aire du triangle $OCA$~? \alph\ Quelle est, en fonction de $a$, l'aire du triangle $OBS$~? \alph\ Quelle est, en fonction de $a$, l'aire du trapère $BCAS$~? \alph\ En déduire $\cal B$ en fonction de $a$. \itemnum Calculer l'aire $\cal A$ en fonction de $a$. \itemnum Montrer la propriété cherchée.} \setbox \tmponebox = \vbox{% \superboxit{0pt}{\vbox to 80truemm{% \hsize = 55truemm \hskip \hsize \vfill }}} \line{\box \tmpbox \hfill \box \tmponebox} \finexo