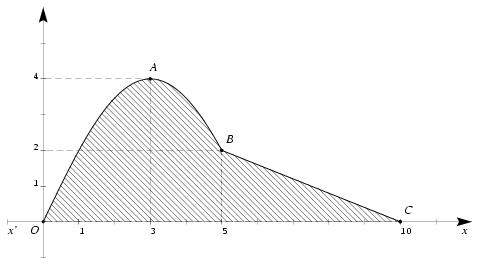
\exo {Volume d'une toupie} Le but de cet exercice est de calculer le volume d'une toupie. On obtient un modèle réduit de cette toupie par rotation autour de l'axe des abscisses $(xx')$ de la surface hachurée ci-après (le modèle réduit représente la toupie en position \og couchée \fg ). % \def \epspath {% $HOME/tex_doc/lycee/database/term/sti/analyse/integr/} \epsfxsize = 120mm % $$ \superboxepsillustrate {vol_004.ps} $$ L'unité graphique est de 1~cm. On donne les quatre points $A (3, 4)$, $B (5, 2)$, $C (10, 0)$ et $D (5, 0)$. La partie inférieure du modèle réduit est le cône de révolution engendré par le triangle $BCD$. La partie supérieure du modèle réduit est engendrée par la surface limitée par une courbe $\Gamma $ ayant l'allure générale du schéma et vérifiant les conditions suivantes~: \itemitem {$\bullet $} La courbe $(\Gamma )$ passe par les points $O$, $A$ et $B$ \itemitem {$\bullet $} La courbe $(\Gamma )$ a une tangente horizontale au point $A$. \itemnum Vérifier que la courbe d'équation $$ y = 4 \sin \left( {\pi x \over 6}\right) \qquad \hbox {($x$ variant de 0 à 5)} $$ remplit ces conditions. On admet dans la suite que c'est la courbe $\Gamma $. \itemitemalphnum En utilisant la formule donnant le volume d'un cône de révolution ou bien en introduisant la fonction dont la courbe représentative est le segment $[BC]$, calculer le volume en cm$^3$ de la partie inférieure du modèle réduit. \itemitemalph Linéariser $\displaystyle {\sin ^2 \left( {\pi x \over 6}\right) }$, puis calculer le volume en cm$^3$ de la partie supérieure du modèle réduit. \itemnum Sachant que la hauteur $OC$ de la toupie en vraie grandeur est de 30~cm, calculer la valeur exacte du volume en cm$^3$ de cette toupie, puis en donner une valeur approchée $0, 1$~cm$^3$ près. {\narrower \narrower {\bf NB~:} \sl On rappelle que~: si $f$ est une fonction continue et positive sur $[a, b]$, et si $E$ est l'ensemble des points $M (x, y)$ du plan tels que $a\leq x \leq b$ et $0\leq y \leq f (x)$, alors le volume $V$ d'un solide de révolution engendré par la rotation de $E$ autour de $xx'$ est~: $$ V = \pi \int _a^b \left[ f (x)\right] ^2 \, dx. $$ \par } \finexo \corrige {} \itemnum Introduisons la fonction $f$. Si $$ f (x) = 4 \sin \left( {\pi x \over 6}\right) \qquad {\rm alors} \qquad f' (x) = {4\pi \over 6} \cos \left( {\pi x \over 6}\right) = \dresultat {{2\pi \over 3} \cos \left( {\pi x \over 6}\right) = f' (x)} $$ Il vient alors $$\displaylines { f (0) = 4 \sin (0) = 0 \quad \Longrightarrow \quad \tresultat {$\Gamma $ passe par $O (0, 0)$} \cr f (3) = 4 \sin \left( {\pi \over 2}\right) = 4 \quad \Longrightarrow \quad \tresultat {$\Gamma $ passe par $A (3, 4)$} \cr f (5) = 4 \sin \left( {5\pi \over 6}\right) = 4 \times {1\over 2} = 2 \quad \Longrightarrow \quad \tresultat {$\Gamma $ passe par $B (5, 2)$} \cr f' (3) = {2\pi \over 3} \cos \left( {\pi \over 2}\right) = 0 \quad \Longrightarrow \quad \tresultat {$\Gamma $ admet une tangente horizontale au point d'abscisse 3} \cr }$$ Ainsi \tresultat {les 4 conditions sont vérifiées}. \itemalphnum {\bf 1ère méthode~:} on utilise la formule qui donne le volume d'un cône de révolution~: $$ V = {\pi R^2 h\over 3} \qquad {\rm soit\ ici} \qquad \dresultat {V_1 = {20\pi \over 3} \cm ^3} $$ \item {} {\bf 2ème méthode~:} on introduit la fonction $g$ dont la courbe représentative est le segment $[BC]$. Comme c'est un segment de droite, la fonction $g$ est affine et a une écriture de la forme $g (x) = ax+b$ où $a$ et $b$ sont des constantes réelles. On trouve $$ \eqalign { \dresultat {g (x) = -{2\over 5} x + 4} \qquad {\rm d'où} \qquad V_1 &= \pi \int _5^{10} \left( -{2\over 5} x + 4\right) ^2 \, dx = \pi \int _5^{10} \left( {4\over 25} x^2 -{16\over 5} x + 16\right) \, dx \cr &= \pi \left[ {4\over 3\times 25} x^3 -{8\over 5} x^2 + 16x\right] _5^{10} \cr &= \pi \left( \left( {160\over 3} - 160 + 160 \right) - \left( {20\over 3} - 40 + 80 \right) \right) = \dresultat {{20\pi \over 3} \cm ^3} \cr }$$ \itemalph On trouve cette linéraisation dans le formulaire~: \dresultat {\sin ^2 \left( {\pi x \over 6}\right) = {1\over 2} \left( 1 - \cos \left( {\pi x \over 3}\right) \right) }. Or le volume $V_2$ de la partie supérieure du modèle réduit vérifie $$\displaylines { \eqalign { V_2 &= \pi \int _0^5 4^2 \sin ^2 \left( {\pi x \over 6}\right) \, dx = \pi \int _0^5 {16\over 2} \left( 1 - \cos \left( {\pi x \over 3}\right) \right) \, dx \cr &= 8\pi \times \int _0^5 \left( 1 - \cos \left( {\pi x\over 3}\right) \right) \, dx \cr &= 8\pi \times \left[ x - {3\over \pi} \sin \left( {\pi x\over 3}\right) \right] _0^5 \cr &= 8\pi \times \left( 5 - {3\over \pi} \sin \left( {5\pi \over 3}\right) - \left( - {3\over \pi} \sin 0 \right) \right) = 8\pi \left( 5 + {3\over \pi }\times {\sqrt 3\over 2}\right) \cr } \cr {\rm soit} \qquad \dresultat {V_2 = \left( 40\pi + 12\sqrt 3\right) \cm ^3} \cr }$$ \itemnum L'échelle entre le modéle réduit et le modèle réel est de 1 à 3. On a donc 1~cm pour 3~cm, 1~cm$^2$ pour $3^2$~cm$^2$, et 1~cm$^3$ pour $3^3$~cm$^3$. D'où le volume de la toupie en vraie grandeur~: $$ V = 27 \times (V_1 + V_2) \cm ^3 \qquad {\rm soit} \qquad \dresultat {V = (1\, 260 \pi +324\sqrt 3) \cm ^3 \approx 4\, 519, 6 \cm ^3} $$ \fincorrige