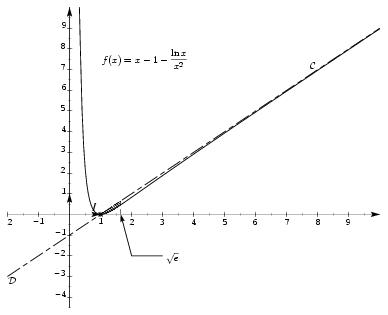
\exo {\' Etude d'une fonction logarithme {\sl bac sti gm, juin 2002}} \let \partie \centerpartie \partie {A -- \' Etude du signe de $x^3 - 1 + 2\ln x$} Soit $g$ la fonction définie sur $]0; +\infty [$ par~: $$ g (x) = x^3 - 1 + 2\ln x. $$ \itemnum Calculer $g' (x)$ et étudier son signe. \itemnum Dresser le tableau de variation de la fonction $g$. (Les limites ne sont pas demandées.) \itemnum Calculer $g (1)$. \itemnum Déduire des questions précédentes le signe de $g (x)$ sur $]0; +\infty [$. \partie {B -- Courbe représentative d'une fonction et calcul d'aire} On considère la fonction $f$ définie sur $]0; +\infty [$ par~: $$ f (x) = x - 1 - {\ln x\over x^2}. $$ On appelle $\cal C$ sa courbe représentative dans le plan rapporté à un repère orthogonam $(O, \vec \imath , \vec \jmath \/)$ (unités~: $3\cm $ sur l'axe des abscisses et $2\cm $ sur l'axe des ordonnées.) \itemitemalphnum Déterminer $\displaystyle { \lim _{x\to +\infty } f (x) }$ et $\displaystyle { \lim _{x\to 0 } f (x) }$. \itemitemalph Montrer que la droite $\cal D$ d'équation $y = x - 1$ est asymptote oblique à $\cal C$. Y a-t-il une autre asymptote à $\cal C$~? Si oui donner son équation. \itemitemalph Calculer $f' (x)$ et montrer que l'on peut écrire $$ f' (x) = {g (x) \over x^3}. $$ \itemitemalph En utilisant les résultats de la partie {\bf A }, déterminer le signe de $f' (x)$, puis dresser le tableau de variation de la fonction $f$. \itemitemalph Calculer les coordonnées du point d'intersection entre l'asymptote $\cal D$ et la courbe $\cal C$. \' Etudier la position de la courbe $\cal C$ par rapport à la droite $\cal D$. \itemitemalph Tracer dans le repère $(O, \vec \imath, \vec \jmath \/)$ la courbe $\cal C$ et la droite $\cal D$. \itemitemalphnum Montrer que la fonction $H$ définie par~: $$ H (x) = - {1\over x} (1 + \ln x) $$ est une primitive de la fonction $h$ définie sur $]0; +\infty [$ par~: $$ h (x) = {\ln x\over x^2}. $$ \itemitemalph Soit $\Delta $ le domaine plan limité par $\cal D$, $\cal C$ et les droites d'équation $x=1$ et $x=\sqrt e$. Hachurer $\Delta $. Calculer la valeur exacte de l'aire, en $\cm ^2$, de $\Delta $ puis en donner une valeur approchée au $\mm ^2$ près. \finexo \corrige \let \partie \llappartie \partie {A} %% \vskip -8mm % \itemnum Il vient \dresultat {g' (x) = 3x^2 + {2\over x}}. Et comme $x$ est strictement positif (puisque l'intervalle de définition de $g$ est $]0;+\infty [$), on en déduit que \tresultat {$g' (x)$ est toujours positif}, comme somme de termes positifs. \itemnum \num \ \num \ On trouve \dresultat {g (1) = 0}, ce qui nous donne alors le tableau récapitulatif suivant~: $$\vcenter {\halign {\offinterlineskip %% preamble \cc {#}& #\tv && # \cr $x$&& $-\infty $&& \hskip .2em $1$&& $+\infty $ \cr \noalign {\hrule } $g' (x)$&& && \hskip .2em $+$& \cr \noalign {\hrule } \bup {\down {$g (x)$}}&&& \brightuparrow & \hss \bup {\down {$0$}}\hss & \bup {\brightuparrow } \cr \noalign {\hrule } signe de $g (x)$&&& \cc {$-$}& \hskip .5em\tv & \cc {$+$} \cr \noalign {\hrule } }} $$ \partie {B} %% \vskip -5mm %% \itemalphnum En $+\infty $, il vient $$ \lim _{x\to +\infty } f (x) = \lim _{x\to +\infty } x - 1 - {\ln x\over x^2} \qquad {\rm soit} \qquad \dresultat {\lim _{x\to +\infty } f (x) = +\infty } $$ puisque $$ \lim _{x\to +\infty } x-1 = +\infty \qquad {\rm et} \qquad \lim _{x\to +\infty } {\ln x \over x^2} = 0 \quad \hbox {d'après le cours}. $$ \item {} Et en $0$, il vient $$ \lim _{x\to 0} f (x) = \lim _{x\to 0^+} x - 1 - {\ln x\over x^2} \qquad {\rm soit} \qquad \dresultat {\lim _{x\to 0^+} f (x) = +\infty } $$ puisque $$ \lim _{x\to 0} x-1 = -1 \qquad \qquad \lim _{x\to 0^+} \ln x = -\infty \qquad \qquad \lim _{x\to 0^+} x^2 = 0^+ \qquad {\rm et} \qquad \lim _{x\to 0^+} {\ln x\over x^2} = -\infty $$ \itemalph De la limite de $f (x)$ en $0$, on en déduit que \tresultat {la droite d'équation $x= 0$ est asymptote verticale} à la courbe de $f$. Et on a bien la droite \tresultat {$y=x-1$ asymptotote oblique} puisque $$ \lim _{x\to +\infty} f (x) - (x-1) = \lim _{x\to +\infty} x - 1 + {\ln x \over x^2} - (x-1) = \lim _{x\to +\infty} {\ln x \over x^2} = 0 \quad \hbox {d'après le cours}. $$ \itemalph Comme $$ f (x) = x - 1 + {\ln x \over x^2} \qquad \hbox {il vient} \qquad f' (x) = 1 + {x^2/x - 2x\ln x\over x^4} = 1 + {x - 2x\ln x\over x^4} = {x^3\over x^3} + {1 - 2\ln x\over x^3} $$ donc on a bien \dresultat {f' (x) = {g (x)\over x^3}}. \itemalph Reste à dresser le tableau de signe de la dérivée $f$ pour obtenir le tableau de variation de $f$~: $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& 0&& 1&& +\infty \cr \noalign {\hrule height 1pt } g (x)&& & -& 0& + \cr \noalign {\hrule } x^3&& 0& +& \tv & + \cr \noalign {\hrule height 1pt} f' (x)&& \doublevrule & -& 0& + \cr \noalign {\hrule height 1pt} \buucenter {$f (x)$}&& \buup {$+\infty $}& \brightddownarrow & \down{$0$}& \brightuuparrow & \buup {$+\infty $} \cr }} }$$ \itemalph Chercher l'intersection entre l'asymptote oblique et la courbe de $f$ revient à résoudre le système $$\displaylines { \cases { y = x-1 \cr y = f (x) \cr } \quad \Longleftrightarrow \quad \cases { y = x-1 \cr x-1 = x-1 - {\ln x \over x^2} \cr } \quad \Longleftrightarrow \quad \cases { y = x-1 \cr 0 = {\ln x \over x^2} \cr } \cr \quad \Longleftrightarrow \quad \cases { y = x-1 \cr 0 = \ln x \cr } \quad \Longleftrightarrow \quad \cases { y = 0 \cr x = 1 \cr } \cr }$$ d'où l'unique point d'intersection~: \dresultat {I (1; 0)}. \item {} Pour les positions relatives, il faut étudier le signe de $f (x) - (x-1)$. En reprenant les calculs précédents, on s'aperçoit que ce signe est celui de $-\ln x$ puisque $f (x) - (x-1) = -(\ln x)/x^2$ avec $x^2$ toujours positif. D'où le tableau récapitulatif suivant~: $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& 0&& 1&& +\infty \cr \noalign {\hrule height 1pt } -\ln x&& & +& 0& - \cr \noalign {\hrule height 1pt} f (x) - (x-1)&& & +& 0& - \cr \noalign {\hrule height 1pt} && & \hbox {$\cal C$ au dessus de $\cal D$}& \tv & \hbox {$\cal C$ au dessous de $\cal D$}& \cr }} }$$ \itemalphnum Comme $$ H (x) = -{1\over x} (1+\ln x), \quad \hbox {il vient} \quad H' (x) = {1\over x^2} (1+\ln x) -{1\over x} \times {1\over x} = {\ln x\over x^2}. $$ Ce qui prouve que \tresultat {$H$ est une primitive de $\displaystyle { {\ln x\over x^2} }$}. \itemalph L'unité d'aire est de \dresultat {3\times 2 = 6\cm^2}. Par définition de l'intégrale, et comme la courbe $\cal C$ est au dessous de $\cal D$ sur l'intervalle $[1; \sqrt e]$, on aura $$ \Delta = 6 \times \int _1^{\sqrt e} (x-1) - f (x) \, dx = 6 \times \int _1^{\sqrt e} {\ln x\over x^2}\, dx = 6 \times \Big[ H (x)\Big] _1^{\sqrt e} = 6 \times \big( H (\sqrt e) - H (1) \big) $$ Comme $H (1) = -1$ et que $H (\sqrt e) = -3/2\sqrt e$ (puisque $\sqrt e = e^{1/2}$, et donc $\ln \sqrt e = 1/2$), il vient $$ \Delta = 6\times \left( -{3\over 2\sqrt e} + 1 \right) \qquad {\rm soit} \qquad \dresultat {\Delta = -{9\over \sqrt e} + 6 \approx 0, 54\cm ^2 \approx 54\mm ^2} $$ \item {} \def \epspath {% $HOME/tex_doc/lycee/database/term/sti/analyse/ln/} $$ \superboxepsillustrate {pbm_013.ps} $$ \fincorrige