%% auteur : JJ Bataille qui n'aurait pu rien faire sans JP Vignault et
%% tous les autres....

4 setxyrapport
140 setxunit
7.5 setborder
90 setangle_repere
-1 2.5 setxrange
-2 12 setyrange
1 1 settkstep
.5 .5 setsubtkstep
2 2 setmkstep
ticks
subticks
marks
traceaxes
unites

%%%% L'équation différentielle y'=y+x avec la condition initiale %%%%y(0)=1 sur lintervalle [0;2]%%%%

%%% La foction solution%%%%%%%%%
/f {setxvar
#rpn#   2*e^x-x-1
} def

%%%%%%%%% Paramètres pour l'approx par la méthode d'Euler%%%%%%%
/nb 4 def	     %%%nbre d'intervalles de subdivision
/pas {2 nb div} def  %%%calcul du pas de la subdivision
/x0 {0} def          %% coordonnees du point a l'origine
/y0 {1} def
/a  {0} def          %% intervalle de calcul = [a;b]
/b  {2} def

%%%%% L'exécutable qui calcule (x_k+1, y_k+1) en fonction de (x_k,y_k)%%%%%%

/F {
2 dict begin
   /y exch def
   /x exch def
#rpn# y + x
end
} def

%%%%%%%% première execution et tracé en rouge %%%%%%%%%%
rouge
[a b {F} x0 y0 pas Euler ] ligne  

%%%%%%%%% deuxième exécution et tracé en vert %%%%%
/nb 20 def
vert
[a b {F} x0 y0 pas Euler ] ligne  

%%%%%%%%%% Tracé de C_f en bleu %%%%%%%%%%  
bleu
0 2  {f} Courbe

%%%%%%%%% Labels %%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%% Label 1 %%%
<latex>
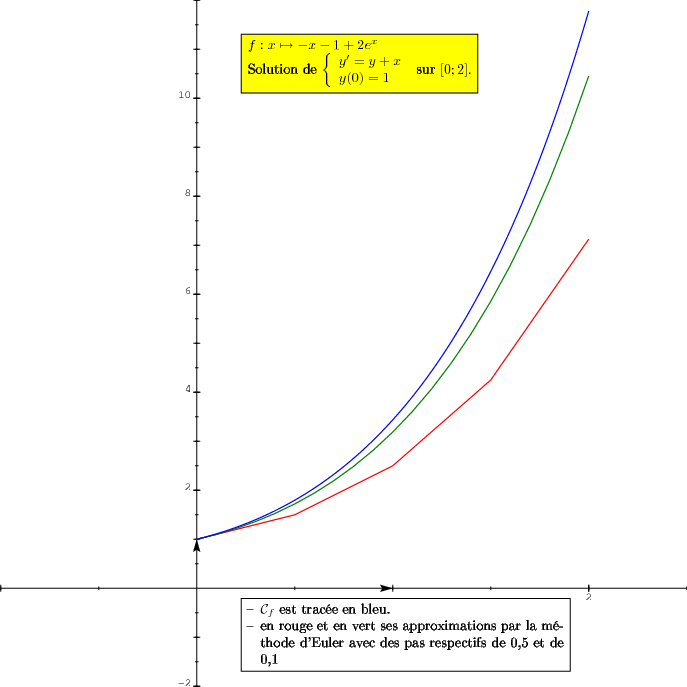
$f:x\mapsto -x-1+2e^x$\\
Solution de $\left\{\begin{array}{l}
y'=y+x\\
y(0)=1 
\end{array}\right.\mbox{ sur } [0;2]. $
</latex>
noir
/fillstyle {jaune fill} def
boxit
0.2 10 urtexlabel
%%%%%%%% Label 2 %%%%%%%
<latex>
\begin{minipage}{8 cm}{
\begin{itemize}
\item $\mathcal{C}_f$ est  tracée en bleu.
\item en rouge et en vert ses approximations
par la méthode d'Euler avec des pas respectifs de 0,5 et de 0,1
\end{itemize}}
\end{minipage}
</latex>

/fillstyle {} def
boxit
0.2 -1.8 urtexlabel