%@metapost:bordeaux1996.mp
%@Titre: Bordeaux -- 1996
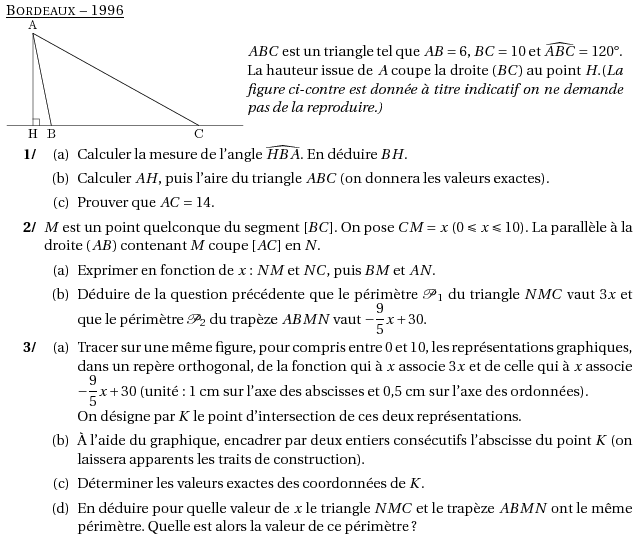
\par\compo{3}{bordeaux1996}{1}{$ABC$ est un triangle tel que $AB=6$, $BC=10$ et $\widehat{ABC}=120$\degres. La hauteur issue de $A$ coupe la droite $(BC)$ au point $H$.{(\em La figure ci-contre est donnée à titre indicatif on ne demande pas de la reproduire.)}
}
\begin{myenumerate}
\item
\begin{enumerate}
\item Calculer la mesure de l'angle $\widehat{HBA}$. En déduire $BH$.
\item Calculer $AH$, puis l'aire du triangle $ABC$ (on donnera les valeurs exactes).
\item Prouver que $AC=14$.
\end{enumerate}
\item $M$ est un point quelconque du segment $[BC]$. On pose $CM=x$ $(0\leqslant x\leqslant10)$. La parallèle à la droite $(AB)$ contenant $M$ coupe $[AC]$ en $N$.
\begin{enumerate}
\item Exprimer en fonction de $x$ : $NM$ et $NC$, puis $BM$ et $AN$.
\item Déduire de la question précédente que le périmètre ${\cal P}_1$ du triangle $NMC$ vaut $3x$ et que le périmètre ${\cal P}_2$ du trapèze $ABMN$ vaut $-\dfrac95x+30$.
\end{enumerate}
\item
\begin{enumerate}
\item Tracer sur une même figure, pour  compris entre 0 et 10, les représentations graphiques, dans un repère orthogonal, de la fonction qui à $x$ associe $3x$ et de celle qui à $x$ associe $-\dfrac95x+30$ (unité : 1~cm sur l'axe des abscisses et 0,5~cm sur l'axe des ordonnées).\par On désigne par $K$ le point d'intersection de ces deux représentations.
\item \`A l'aide du graphique, encadrer par deux entiers consécutifs l'abscisse du point $K$ (on laissera apparents les traits de construction).
\item Déterminer les valeurs exactes des coordonnées de $K$.
\item En déduire pour quelle valeur de $x$ le triangle $NMC$ et le trapèze $ABMN$ ont le même périmètre. Quelle est alors la valeur de ce périmètre ?
\end{enumerate}
\end{myenumerate}