%@metapost:4espaceexo34.mp
%@Auteur:Régis Gary\par
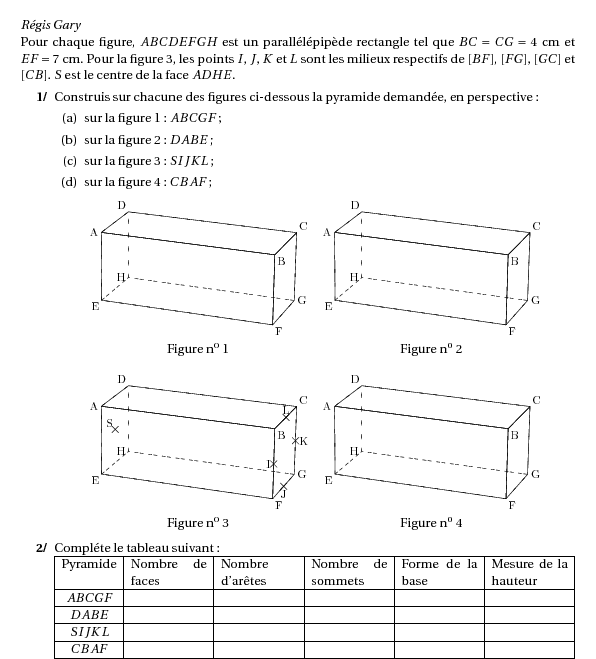
Pour chaque figure, $ABCDEFGH$ est un parallélépipède rectangle tel
que $BC=CG=4$~cm et $EF=7$~cm. Pour la figure 3, les points $I$, $J$,
$K$ et $L$ sont les milieux respectifs de $[BF]$, $[FG]$, $[GC]$ et
$[CB]$. $S$ est le centre de la face $ADHE$.
\begin{myenumerate}
  \item Construis sur chacune des figures ci-dessous la pyramide
    demandée, en perspective :
    \begin{enumerate}
    \item sur la figure 1 : $ABCGF$;
    \item sur la figure 2 : $DABE$;
    \item sur la figure 3: $SIJKL$;
    \item sur la figure 4: $CBAF$;
    \end{enumerate}
    \begin{center}
      \begin{tabular}{cc}
        \includegraphics{4espaceexo34.1}&\includegraphics{4espaceexo34.1}\\
        Figure \no1&Figure \no2\\
        \\
        \includegraphics{4espaceexo34.2}&\includegraphics{4espaceexo34.1}\\
        Figure \no3&Figure \no4\\
      \end{tabular}
    \end{center}
  \item Compléte le tableau suivant :\\
    \begin{tabularx}{\linewidth}{|c|X|X|X|X|X|}
      \hline
      Pyramide&Nombre de faces&Nombre d'arêtes&Nombre de sommets&Forme
      de la base&Mesure de la hauteur\\
      \hline
      $ABCGF$&&&&&\\
      \hline
      $DABE$&&&&&\\
      \hline
      $SIJKL$&&&&&\\
      \hline
      $CBAF$&&&&&\\
      \hline
    \end{tabularx}
\end{myenumerate}