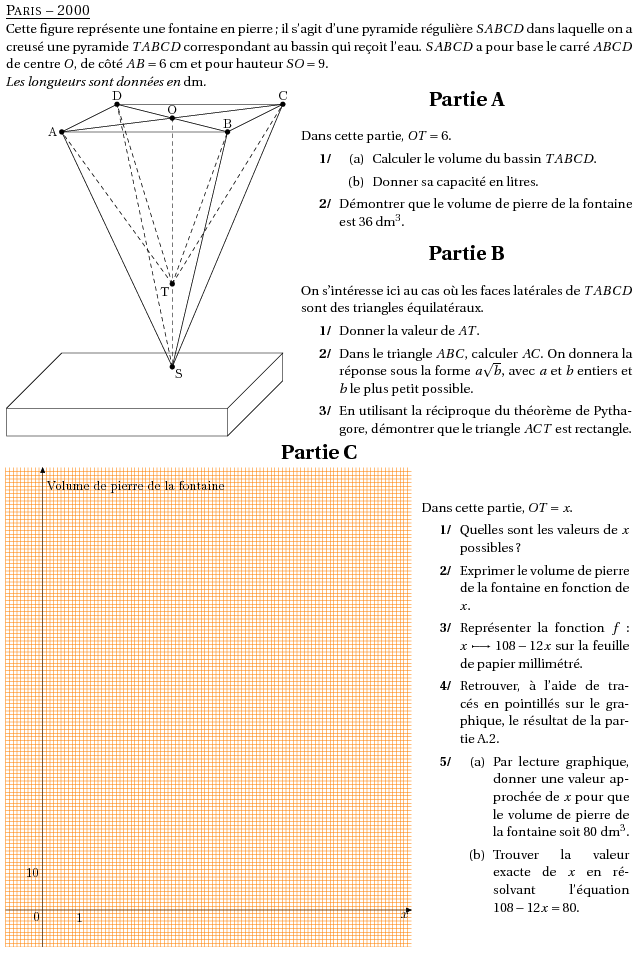
%@metapost:paris2000.mp %@Titre: Paris -- 2000 \small Cette figure représente une fontaine en pierre ; il s'agit d'une pyramide régulière $SABCD$ dans laquelle on a creusé une pyramide $TABCD$ correspondant au bassin qui reçoit l'eau. $SABCD$ a pour base le carré $ABCD$ de centre $O$, de côté $AB=6$~cm et pour hauteur $SO=9$. \textit{Les longueurs sont données en {\em dm}.} \par\compo{5}{paris2000}{1}{ \begin{center} \textbf{\Large{Partie A }} \end{center} Dans cette partie, $OT=6$. \begin{myenumerate} \item \begin{enumerate} \item Calculer le volume du bassin $TABCD$. \item Donner sa capacité en litres. \end{enumerate} \item Démontrer que le volume de pierre de la fontaine est 36~dm$^3$. \end{myenumerate} \begin{center} \textbf{\Large{Partie B }} \end{center} On s'intéresse ici au cas où les faces latérales de $TABCD$ sont des triangles équilatéraux. \begin{myenumerate} \item Donner la valeur de $AT$. \item Dans le triangle $ABC$, calculer $AC$. On donnera la réponse sous la forme $a\sqrt{b}$, avec $a$ et $b$ entiers et $b$ le plus petit possible. \item En utilisant la réciproque du théorème de Pythagore, démontrer que le triangle $ACT$ est rectangle. \end{myenumerate} } \begin{center} \textbf{\Large{Partie C }} \end{center} \par\compo{6}{paris2000}{1}{Dans cette partie, $OT=x$. \begin{myenumerate} \item Quelles sont les valeurs de $x$ possibles ? \item Exprimer le volume de pierre de la fontaine en fonction de $x$. \item Représenter la fonction $f : x \longmapsto 108-12x$ sur la feuille de papier millimétré. \item Retrouver, à l'aide de tracés en pointillés sur le graphique, le résultat de la partie A.2. \item \begin{enumerate} \item Par lecture graphique, donner une valeur approchée de $x$ pour que le volume de pierre de la fontaine soit 80~dm$^3$. \item Trouver la valeur exacte de $x$ en résolvant l'équation $108-12x=80$. \end{enumerate} \end{myenumerate} }