

On note 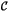 l'ensemble des points de coordonnées
l'ensemble des points de coordonnées 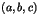 où
où
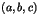 est un trio.
est un trio.
On note 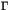 l'ensemble des points de coordonnées
l'ensemble des points de coordonnées 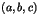 où
où
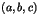 est un trio réduit.
est un trio réduit.
On note 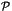 le plan d'équation
le plan d'équation 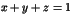 .
.
- Existe-t-il des trios
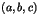 tels que
tels que 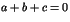 ?
?
- Montrer que
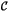 est une réunion de droites passant par
est une réunion de droites passant par 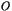 et privées de ce point.
et privées de ce point.
- Montrer que
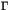 est l'intersection d'un plan et d'une sphère de
centre
est l'intersection d'un plan et d'une sphère de
centre 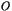 . Quelle est la nature géométrique de
. Quelle est la nature géométrique de 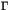 ?
?
- Donner la nature géométrique de
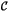 et l'illustrer d'un
croquis.
et l'illustrer d'un
croquis.
- Soit
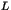 un point fixé de
un point fixé de 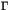 .
Montrer que le volume
.
Montrer que le volume 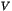 du tétraèdre
du tétraèdre 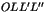 , où
, où 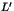 et
et 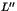 sont
deux points distincts de
sont
deux points distincts de 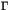 et différents de
et différents de 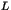 , est maximal lorsque
les arêtes issues de
, est maximal lorsque
les arêtes issues de 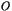 sont deux à deux orthogonales et déterminer alors
les coordonnées de
sont deux à deux orthogonales et déterminer alors
les coordonnées de 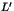 et
et 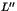 en fonction de celles de
en fonction de celles de 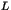 .
.
- Montrer que le produit
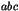 admet un maximum et un minimum lorsque
le point de coordonnées
admet un maximum et un minimum lorsque
le point de coordonnées 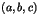 décrit
décrit 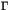 . Préciser les trios
réduits réalisant ces extremums.
. Préciser les trios
réduits réalisant ces extremums.
2001-03-08
![]() l'ensemble des points de coordonnées
l'ensemble des points de coordonnées ![]() où
où
![]() est un trio.
est un trio.
![]() l'ensemble des points de coordonnées
l'ensemble des points de coordonnées ![]() où
où
![]() est un trio réduit.
est un trio réduit.
![]() le plan d'équation
le plan d'équation ![]() .
.