

Dans cette partie et les suivantes, un trio 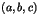 est dit
rationnel lorsque
est dit
rationnel lorsque 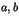 et
et 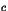 sont des nombres rationnels
(éléments de l'ensemble
sont des nombres rationnels
(éléments de l'ensemble  ) ; Il est dit entier, lorsque
) ; Il est dit entier, lorsque 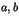 et
et 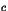 sont des nombres entiers relatifs (éléments de l'ensemble
sont des nombres entiers relatifs (éléments de l'ensemble  ) ;
enfin un trio entier est dit primitif si
) ;
enfin un trio entier est dit primitif si 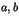 et
et 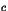 n'admettent
que
n'admettent
que 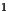 et
et  comme diviseurs communs.
comme diviseurs communs.
- Déterminer la nature de l'ensemble
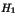 des points de coordonnées
des points de coordonnées
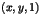 tels que
tels que 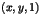 soit un trio. Montrer que le point
soit un trio. Montrer que le point 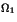 de coordonnées
de coordonnées 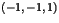 est un centre de symétrie de
est un centre de symétrie de 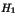 . Quels sont
les points de
. Quels sont
les points de 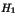 à coordonnées entières ?
à coordonnées entières ?
- Pour tout entier naturel non nul
 , on note
, on note  l'ensemble des
trios entiers
l'ensemble des
trios entiers 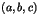 tels que
tels que  . Déterminer
. Déterminer  pour
pour  et
et
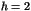 .
.
- Montrer que
 est un ensemble fini et exprimer le nombre
est un ensemble fini et exprimer le nombre  de ses éléments en fonction de celui des diviseurs de
de ses éléments en fonction de celui des diviseurs de  dans
dans  .
Montrer que
.
Montrer que 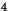 divise
divise 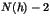 .
.
- Pour tout entier naturel non nul
 , on note
, on note  le nombre des
trios entiers
le nombre des
trios entiers 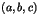 tels que l'un au moins des entiers
tels que l'un au moins des entiers 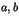 ou
ou 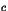 soit égal à
soit égal à  ? Exprimer
? Exprimer  en fonction de
en fonction de  selon la parité de
selon la parité de
 .
.
- Montrer qu'à tout trio entier
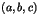 on peut associer un triplet
on peut associer un triplet
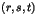 d'entiers tels que
d'entiers tels que  et
et  soient premiers entre eux,
soient premiers entre eux,  positif ou nul et tels que l'on ait :
positif ou nul et tels que l'on ait :  ,
,  ,
,  .
.
Énoncer et démontrer une réciproque. Pour quels trios 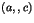 le triplet
le triplet
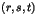 n'est-il pas unique ?
n'est-il pas unique ?
- Déterminer les triplets
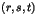 ainsi associés aux trios primitifs.
En déduire que si
ainsi associés aux trios primitifs.
En déduire que si 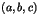 est un trio primitif, alors
est un trio primitif, alors
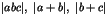 , et
, et 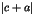 sont des carrés d'entiers.
sont des carrés d'entiers.
- pour tout entier naturel non nul
 , on note
, on note  le nombre de
trios primitifs
le nombre de
trios primitifs 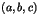 tels que
tels que  . Montrer que
. Montrer que  est une
puissance de
est une
puissance de  . Pour quels entiers
. Pour quels entiers  a-t-on
a-t-on  ? Expliciter
une suite d'entiers
? Expliciter
une suite d'entiers  tels que la suite
tels que la suite
 converge vers zéro.
converge vers zéro.
- Soit
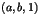 un trio. Montrer qu'il existe deux suites
un trio. Montrer qu'il existe deux suites 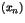 et
et
 convergeant respectivement vers
convergeant respectivement vers  et
et  et telles que pour tout
et telles que pour tout
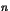 ,
, 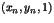 soit un trio rationnel.
soit un trio rationnel.
- Soit
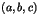 un trio réduit. Montrer qu'il existe trois suites
un trio réduit. Montrer qu'il existe trois suites
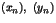 et
et  convergeant respectivement vers
convergeant respectivement vers 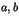 et
et 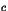 et
telles que pour tout
et
telles que pour tout 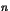 ,
, 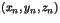 soit un trio rationnel réduit.
soit un trio rationnel réduit.


2001-03-08
![]() est dit
rationnel lorsque
est dit
rationnel lorsque ![]() et
et ![]() sont des nombres rationnels
(éléments de l'ensemble
sont des nombres rationnels
(éléments de l'ensemble ![]() ) ; Il est dit entier, lorsque
) ; Il est dit entier, lorsque ![]() et
et ![]() sont des nombres entiers relatifs (éléments de l'ensemble
sont des nombres entiers relatifs (éléments de l'ensemble ![]() ) ;
enfin un trio entier est dit primitif si
) ;
enfin un trio entier est dit primitif si ![]() et
et ![]() n'admettent
que
n'admettent
que ![]() et
et ![]() comme diviseurs communs.
comme diviseurs communs.