

On note 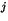 le nombre complexe
le nombre complexe
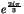 , c'est à dire
, c'est à dire
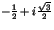 .
.
Pour tout trio 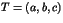 on note
on note
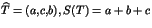 et
et
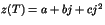 .
.
- Calculer le module de
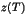 en fonction de
en fonction de 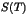 . Peut-on avoir
. Peut-on avoir
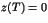 ? Calculer le cosinus et le sinus d'un argument
? Calculer le cosinus et le sinus d'un argument 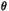 de
de
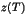 en fonction de
en fonction de 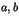 et
et 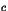 .
.
- Soit
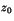 un nombre complexe non nul. Déterminer les trios
un nombre complexe non nul. Déterminer les trios
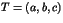 tels que
tels que 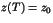 .
.
- Étant donnés deux trios
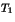 et
et 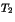 , montrer qu'il existe un
unique trio, noté
, montrer qu'il existe un
unique trio, noté 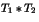 , vérifiant
, vérifiant
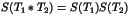 et
et
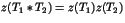 . Calculer
. Calculer 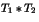 en fonction de
en fonction de 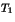 et
et
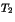 . Que peut-on dire d'un argument de
. Que peut-on dire d'un argument de 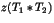 ? Que peut-on dire
d'un argument de
? Que peut-on dire
d'un argument de
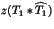 ?
?
- si
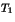 et
et 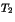 sont réduits, en est-il de même de
sont réduits, en est-il de même de 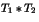 ? Si
? Si
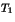 et
et 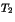 sont entiers, en est-il de même de
sont entiers, en est-il de même de 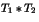 ? Si
? Si 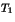 et
et
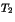 sont primitifs, en est-il de même de
sont primitifs, en est-il de même de 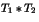 ?
?
- Comparer les trios
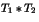 et
et
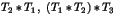 et
et
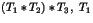 et
et 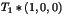 .
.
- Étant donnés les trios
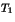 et
et 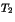 , résoudre l'équation
, résoudre l'équation
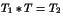 où le trio
où le trio 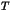 est l'inconnue.
est l'inconnue.
- Étant donné un trio
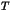 , on définit une suite de trios
, on définit une suite de trios 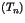 par
par
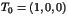 et
et 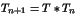 . Calculer
. Calculer 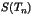 . Étant donné un
entier
. Étant donné un
entier 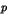 , résoudre l'équation
, résoudre l'équation 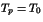 où le trio
où le trio 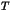 est l'inconnue.
est l'inconnue.
2001-03-08
![]() le nombre complexe
le nombre complexe
![]() , c'est à dire
, c'est à dire
![]() .
.
![]() on note
on note
![]() et
et
![]() .
.