

On note 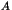 l'ensemble des entiers
l'ensemble des entiers 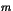 non nuls tels qu'il existe deux
entiers
non nuls tels qu'il existe deux
entiers 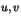 tels que
tels que 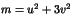 .
.
On note 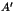 l'ensemble des nombres complexes
l'ensemble des nombres complexes 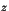 non nuls tels qu'il
existe deux entiers
non nuls tels qu'il
existe deux entiers 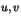 tels que
tels que
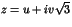 (on remarquera que
(on remarquera que
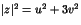 ).
).
On note 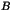 l'ensemble des entiers
l'ensemble des entiers 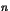 non nuls tels qu'il existe deux
entiers
non nuls tels qu'il existe deux
entiers 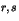 tels que
tels que 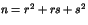 .
.
- Montrer que le produit de deux éléments de
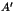 appartient à
appartient à 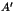 ,
puis que le produit de deux éléments de
,
puis que le produit de deux éléments de 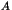 appartient à
appartient à 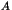 .
.
- Montrer que si
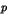 est en nombre premier élément de
est en nombre premier élément de 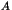 , alors
, alors 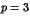 ou
ou 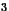 divise
divise 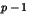 .
.
- Montrer que
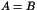 (on pourra notamment remarquer que
(on pourra notamment remarquer que
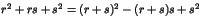 ).
).
- Montrer que
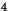 divise les éléments pairs de
divise les éléments pairs de 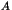 et que les quotients
appartiennent à
et que les quotients
appartiennent à 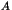 , puis que tout élément de
, puis que tout élément de 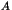 est produit d'un élément
impair de
est produit d'un élément
impair de 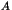 par une puissance de
par une puissance de 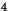 .
.
- Soit s'il en existe, un entier impair
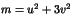 tel que les
entiers
tel que les
entiers 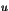 et
et 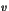 soient premiers entre eux et qui admet un diviseur
premier
soient premiers entre eux et qui admet un diviseur
premier 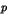 n'appartenant pas à
n'appartenant pas à 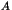 . Montrer qu'il existe alors un plus
petit entier strictement positif
. Montrer qu'il existe alors un plus
petit entier strictement positif 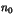 tel que
tel que 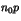 appartienne à
appartienne à 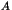 .
Montrer que
.
Montrer que 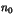 est impair.
est impair.
- Établir l'existence de deux entiers
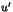 et
et 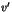 inférieurs en valeur
absolue à
inférieurs en valeur
absolue à 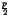 tels que
tels que 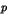 divise
divise 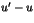 et
et 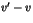 . Montrer que
. Montrer que 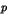 divise l'entier non nul
divise l'entier non nul 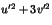 et que
et que 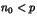 .
.
- Établir l'existence de deux entiers non nuls premiers entre eux
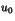 et
et 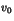 tels que
tels que
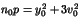 .
.
- Établir l'existence de deux entiers
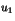 et
et 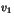 inférieurs en
valeur absolue à
inférieurs en
valeur absolue à 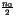 tels que
tels que 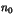 divise
divise 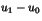 et
et
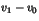 . Montrer que
. Montrer que 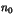 divise l'entier non nul
divise l'entier non nul 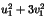 que
l'on notera
que
l'on notera 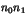 .
.
- En déduire qu'un tel entier
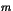 ne peut pas exister (on pourra
considérer l'entier
ne peut pas exister (on pourra
considérer l'entier 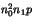 ).
).
- Montrer que tout élément de
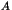 s'écrit
s'écrit
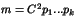 , où
, où
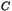 est un entier naturel non nul et les
est un entier naturel non nul et les 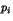 des nombres premiers
distincts éléments de
des nombres premiers
distincts éléments de 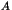 .
.
- Soit
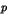 un nombre premier tel que
un nombre premier tel que 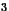 divise
divise 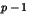 et
et 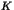 l'ensemble
des triplets
l'ensemble
des triplets 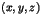 où les entiers
où les entiers 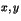 et
et 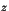 sont strictement compris
entre
sont strictement compris
entre 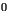 et
et 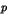 , et tels que
, et tels que 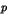 divise (
divise (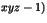 . Montrer que
. Montrer que 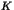 possède
possède 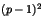 éléments, et que
éléments, et que 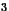 divise le nombre d'éléments de
divise le nombre d'éléments de 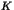 ne vérifiant pas
ne vérifiant pas 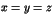 .
.
- En déduire qu'il existe en entier
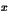 strictement compris entre
strictement compris entre 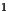 et
et 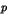 tel que
tel que 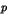 divise
divise 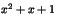 , puis que
, puis que 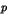 appartient à
appartient à 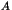 .
Décrire les éléments de
.
Décrire les éléments de 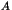 .
.
- Soit
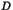 l'ensemble des entiers
l'ensemble des entiers 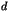 tels qu'il existe un trio entier
tels qu'il existe un trio entier
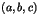 vérifiant
vérifiant 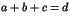 et
et 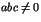 . Montrer, grâce à la question
5/ de la deuxième partie, que tout élément de
. Montrer, grâce à la question
5/ de la deuxième partie, que tout élément de 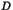 possède un
diviseur premier élément de
possède un
diviseur premier élément de 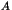 Réciproquement, que peut-on dire d'un
entier non nul admettant un diviseur premier élément de
Réciproquement, que peut-on dire d'un
entier non nul admettant un diviseur premier élément de 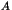 ?
?
- En déduire les éléments de
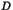 compris aux sens large entre
compris aux sens large entre 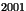 et
et
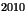 .
.


2001-03-08
![]() l'ensemble des entiers
l'ensemble des entiers ![]() non nuls tels qu'il existe deux
entiers
non nuls tels qu'il existe deux
entiers ![]() tels que
tels que ![]() .
.
![]() l'ensemble des nombres complexes
l'ensemble des nombres complexes ![]() non nuls tels qu'il
existe deux entiers
non nuls tels qu'il
existe deux entiers ![]() tels que
tels que
![]() (on remarquera que
(on remarquera que
![]() ).
).
![]() l'ensemble des entiers
l'ensemble des entiers ![]() non nuls tels qu'il existe deux
entiers
non nuls tels qu'il existe deux
entiers ![]() tels que
tels que ![]() .
.