Exercice - étude de fonction
Jean-Michel Sarlat (jm-sarlat@melusine.eu.org) - 26 avril 2003| 1 | Énoncé | |
| 2 | Corrigé | |
1 - Énoncé

2 - Corrigé
maxima >>
(C2) f(x):=(x*cosh(x)-sinh(x))/(cosh(x)-1);

1/ Un rapide calcul de tête nous indique que le numérateur et le dénominateur de l'expression ![]() sont d'ordre
sont d'ordre ![]() et
et ![]() en
en ![]() au voisinage de
au voisinage de ![]() . Pour obtenir un développement limité à l'ordre
. Pour obtenir un développement limité à l'ordre ![]() en
en ![]() de
de ![]() il faut donc anticiper la simplification par
il faut donc anticiper la simplification par ![]() et développer le numérateur et le dénominateur à l'ordre
et développer le numérateur et le dénominateur à l'ordre ![]() . Enfin, si on devait le faire à la main...
. Enfin, si on devait le faire à la main...
(C3) taylor(f(x),x,0,3);

La limite de ![]() est donc
est donc ![]() , il suffit de poser
, il suffit de poser ![]() pour que
pour que ![]() soit continue en
soit continue en ![]() .
.
(C4) c:limit(f(x)/x,x,0);

2/ ![]() est dérivable en
est dérivable en ![]() (ce que l'on pouvait déduire du développement précédent) et
(ce que l'on pouvait déduire du développement précédent) et ![]() .
.
(C5) taylor(f(x)-c*x,x,0,3);

La différence ![]() est équivalente à
est équivalente à ![]() au voisinage de
au voisinage de ![]() , la courbe représentative de
, la courbe représentative de ![]() traverse donc sa tangente à l'origine, elle passe de dessous au dessus (point d'inflexion).
traverse donc sa tangente à l'origine, elle passe de dessous au dessus (point d'inflexion).
(C6) diff(f(x),x);
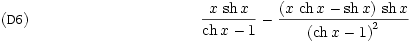
3/ Le signe de la dérivée n'est pas simple à déterminer sous cette forme, on factorise!
(C7) factor(%);

Là, les choses sont plus nettes. La quantité dont le signe n'est pas immédiat est ![]() , on a toutefois vite fait de se convaincre qu'elle est positive sur
, on a toutefois vite fait de se convaincre qu'elle est positive sur ![]() , en s'appuyant sur le signe de sa dérivée qui est manifestement positive. La fonction
, en s'appuyant sur le signe de sa dérivée qui est manifestement positive. La fonction ![]() est croissante sur
est croissante sur ![]() .
.
(C8) a:limit(f(x)/x,x,inf);

(C9) b:limit(f(x)-a*x,x,inf);

4/ Les deux calculs précédents prouvent l'existence d'une droite asymptote à ![]() , son équation est
, son équation est ![]() .
.
(C10) g(x):=f(x)-a*x-b;
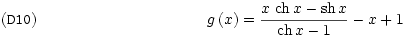
(C11) exponentialize:true$
L'étude de la position de la courbe par rapport à son asymptote au voisinage de ![]() peut être faite en recherchant un équivalent de
peut être faite en recherchant un équivalent de ![]() . Demander, comme cela, un développement de
. Demander, comme cela, un développement de ![]() ne convient pas à maxima, c'est pourquoi on passe à l'écriture à l'aide d'exponentielles des fonctions
ne convient pas à maxima, c'est pourquoi on passe à l'écriture à l'aide d'exponentielles des fonctions ![]() et
et ![]() .
.
(C12) factor(g(x));

La factorisation de ![]() prépare le développement à suivre.
prépare le développement à suivre.
(C13) taylor(%,x,inf,1);

Un équivalent de ![]() au voisinage de
au voisinage de ![]() est
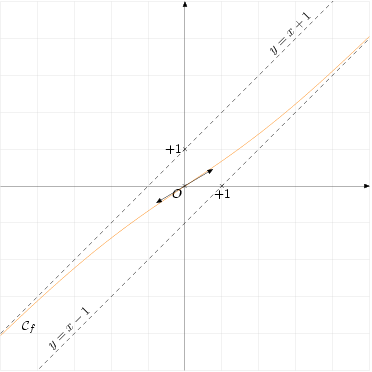
est ![]() qui est positif. La courbe
qui est positif. La courbe ![]() est donc au dessus de son asymptote vers
est donc au dessus de son asymptote vers ![]() .
.
Autres réalisations de ce document : index.pdf, index.ps.
Source index.txt mouliné par petitParseur(Z+B) le samedi 26 avril 2003.