|
On voit souvent dans les villes, lorsque la visibilité à la sortie d’un garage ou à un carrefour est insuffisante, ou bien dans certains magasins pour des motifs de surveillance, des miroirs bombés donnant de l’environnement un panorama très large. On peut prendre aussi une boule argentée ou dorée que l’on suspend aux branches des sapins de Noël, pour voir le décor se réfléchir dans la boule avec une distorsion bien particulière.
L’objectif est de définir des éléments de décor en 3D, des briques, pour reconstruire ce qu’un observateur placé à une certaine distance d’une boule miroir, à la même hauteur que son centre verrait.
Les briques à notre disposition sont :

|
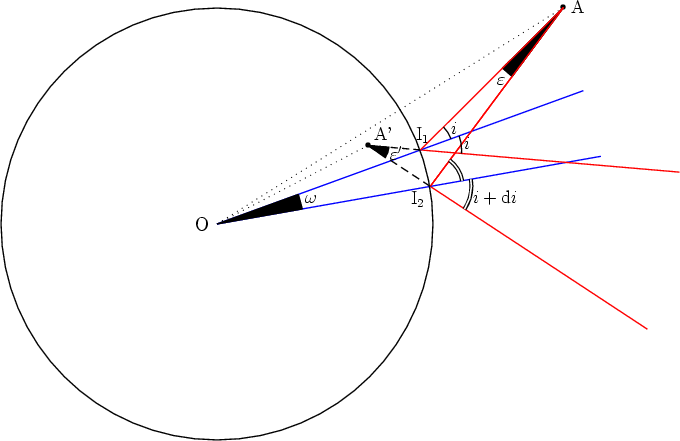
Le point lumineux A, quel qu’il soit, est dans le plan du grand cercle de la sphère défini par OI1A. Je donne le début de cette étude théorique, qui est une adaptation des pages 108 et suivantes de son livre, sans la développer jusqu’à son terme, car comme l’indique Henri Bouasse lui-même « Le problème est généralement inextricable, sauf dans le cas où la symétrie du système indique quels rayons il faut regrouper après réflexion ». Et bien que la fin de cette remarque s’applique au miroir sphérique, encore faudrait-il que les calculs soient facilement programmables et relativement rapides et j’avoue avoir été découragé par leur complexité. Heureusement, nous verrons que dans certaines conditions, de judicieuses approximations permettent d’obtenir une solution réaliste.
Afin d’apprécier la difficulté du problème, on considère d’abord les limites du
pinceau dans ce plan, c’est à dire sur l’arc 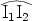 .
.
Les angles sont exagérément grands pour des raisons de clarté.
Dans le triangle OI1A,
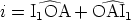
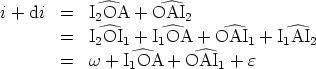
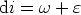 | (1) |
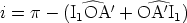
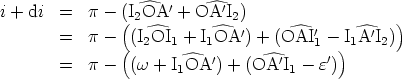
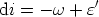 | (2) |
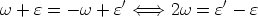 | (3) |
 ,
,  ' et
' et 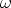 sont de petits angles, on établit les relations
suivantes, en posant :
sont de petits angles, on établit les relations
suivantes, en posant :
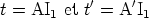
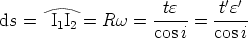
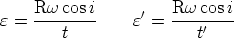
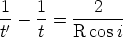
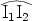 , l’image
virtuelle que verrait l’œil serait A', qui est dans ce plan la trace de la focale
tangentielle.
, l’image
virtuelle que verrait l’œil serait A', qui est dans ce plan la trace de la focale
tangentielle.
Il faut maintenant envisager toutes les autres génératrices du cône. On en prend deux de particulières, celles qui sont sur les bouts de l’arc de cercle de la sphère perpendiculaire au grand cercle précédent. Nous ne pouvons plus nous placer maintenant dans un plan pour faire le schéma. Ces deux génératrices permettent de déterminer la focale radiale A''. Les deux focales A' et A'' sont alignées avec le rayon réfléchi correspondant au rayon moyen du pinceau incident.
En conclusion, à la page 134, Henri Bouasse écrit : « l’œil n’utilise qu’un pinceau extrêmement étroit ; il s’accommode sur l’une des focales ou sur le cercle de diffusion. ». Nous avons un peu avancé, mais quel(s) point(s) calculer?
Les milieux des focales tangentielles, radiales et du cercle de diffusion se trouvent alignés avec l’œil et le point d’incidence du rayon moyen du faisceau (celui qui après réflexion passe par l’œil). L’image obtenue d’un objet quelconque n’est pas plane. On pourrait contourner la difficulté en imaginant un plan fictif perpendiculaire à l’axe œil-centre de la boule et passant par une valeur moyenne des cercles de diffusion, sur lequel on calculerait les intersections des rayons. Il faut bien reconnaître que tout cela est passablement compliqué.
Henri Bouasse propose, dans certaines conditions, une méthode approximative qui donne de bons résultats et qui a l’avantage d'être simple. C’est l’intégralité de cette solution qu’il donne dans les pages 133, 134 et 135 de son livre, qui est développée ci-après.
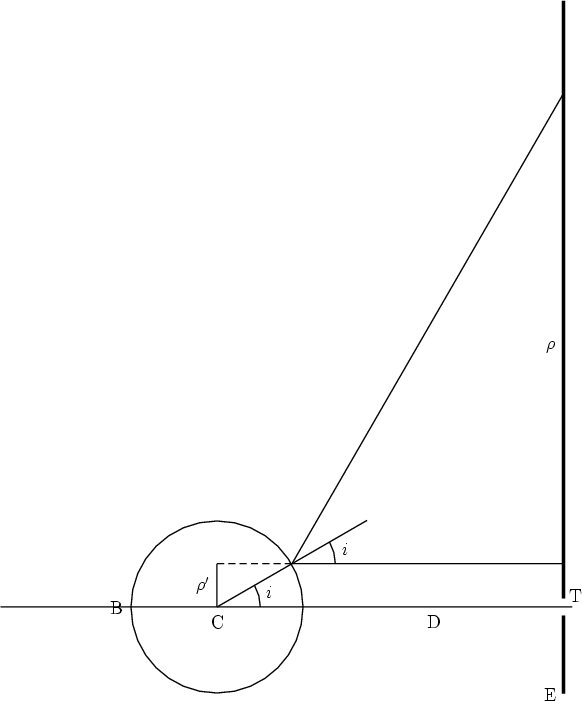
|
Sur une très grande feuille de carton blanc E, on trace un quadrillage en traits noirs épais. On regarde l’image de ce quadrillage par un petit trou percé au centre du carton.
La distance D = TB sera prise d’une trentaine de centimètres.
Le quadrillage apparaît déformé en barillet, mais parfaitement net.
2 o — Pour avoir une idée de la loi de déformation supposons l’œil assez loin pour
que les rayons réfléchis qui y parviennent, soient quasi-parallèles. Appelons 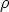 ' la distance
d’un rayon à la droite TB.
' la distance
d’un rayon à la droite TB.
Soit R le rayon de la boule. l’angle d’incidence est :
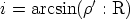
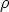 de TB donnée par la
formule :
de TB donnée par la
formule :
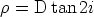
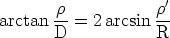
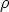 devient infini pour :
devient infini pour :
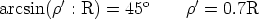

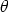 ,
, 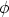 ) lesquelles sont paramétrées, avec des valeurs en degrés avec
:
) lesquelles sont paramétrées, avec des valeurs en degrés avec
:
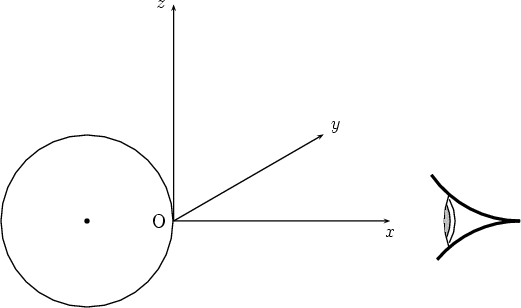
Un vecteur unitaire quelconque a pour coordonnées, en fonction de 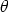 et
et 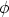 :
:
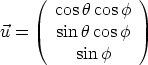
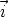 ,
, 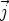 ,
, 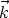 sont les vecteurs unitaires dirigés respectivement suivant Ox, Oy et Oz.
sont les vecteurs unitaires dirigés respectivement suivant Ox, Oy et Oz.
Le vecteur unitaire normal à un plan de front, c’est-à-dire parallèle à Oyz, est le
vecteur 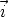 ou -
ou -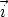 ,
, 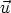 (
(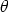 = 0 ou
= 0 ou 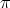 ,
, 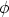 = 0).
= 0).
Un plan horizontal est parallèle à Oxy, un vecteur normal est soit 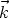 , soit -
, soit -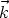 , il est
défini par
, il est
défini par 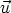 (
(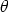 = valeur indifférente(0),
= valeur indifférente(0), 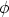 =
= 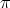 /2 ou -
/2 ou - 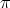 /2).
/2).
Un plan vertical parallèle à Oxz a pour normale 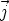 ou -
ou -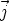 , donc
, donc 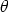 =
= 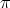 /2 ou -
/2 ou - 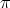 /2 et
/2 et
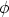 = 0.
= 0.
Une remarque importante : le vecteur unitaire choisi normal au plan 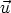 ,
détermine l’orientation des vecteurs
,
détermine l’orientation des vecteurs 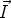 et
et 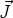 du plan, avec les règles habituelles
d’orientation : le trièdre (
du plan, avec les règles habituelles
d’orientation : le trièdre (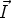 ,
, 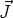 ,
, 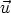 ) est direct, mais le vecteur
) est direct, mais le vecteur 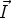 a été pris dans le
plan de référence Oxy.
a été pris dans le
plan de référence Oxy.
Pour que le quadrillage soit parfaitement déterminé, on fixe les valeurs de deux sommets opposé avec : Ymin=-50,Ymax=10,Xmax=70,Xmin=-70. Ainsi que le pas de la grille avec grille=10, par exemple.
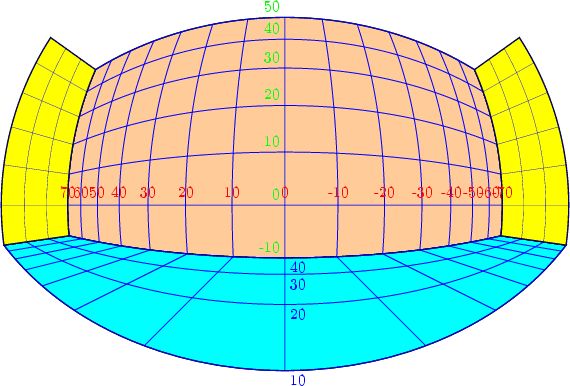
Le quadrillage du plan de front est défini par :
\BouleQuadrillage[normaleLongitude=0,% normaleLatitude=0,% Xorigine=40,Yorigine=0,Zorigine=0,% linecolor=blue,linewidth=0.2mm,grille=10,% Ymin=-50,Ymax=10,Xmax=70,Xmin=-70]% |
\BouleQuadrillage[normaleLongitude=0,% normaleLatitude=90,% Xorigine=40,Yorigine=0,Zorigine=-10,% linecolor=blue,linewidth=0.2mm,grille=10,% Ymin=-30,Ymax=0,Xmax=70,Xmin=-70]% |
\BouleQuadrillage[normaleLongitude=90,% normaleLatitude=0,% Xorigine=40,Yorigine=70,Zorigine=-10,% linecolor=blue,linewidth=0.05mm,grille=10,% Ymin=-60,Ymax=0,Xmin=-30,Xmax=0]% \BouleQuadrillage[normaleLongitude=90,% normaleLatitude=0,% Xorigine=40,Yorigine=-70,Zorigine=-10,% linecolor=blue,linewidth=0.05mm,grille=10,% Ymin=-60,Ymax=0,Xmin=-30,Xmax=0]% |
On obtient la même chose que précédemment en faisant :
\begin{pspicture}(-5,-4)(5,4)
% plan de front
\psset{Boule=false}
{\psset{normaleLongitude=180,%
normaleLatitude=0,%
Xorigine=40,%
Yorigine=0,%
Zorigine=0}
\BouleFrame[fillstyle=solid,fillcolor=OrangePale](-70,-50)(70,10)
\BouleQuadrillage[linecolor=blue,linewidth=0.2mm,grille=10,%
Ymin=-50,Ymax=10,Xmax=70,Xmin=-70]}%
% plan horizontal
{\psset{normaleLongitude=0,%
normaleLatitude=-90,%
Xorigine=40,%
Yorigine=0,%
Zorigine=-10}
\BouleFrame[fillstyle=solid,fillcolor=cyan](70,30)(-70,0)
\BouleQuadrillage[linecolor=blue,linewidth=0.2mm,grille=10,%
Ymin=0,Ymax=30,Xmax=70,Xmin=-70]}%
% plan vertical de gauche
{\psset{normaleLongitude=-90,%
normaleLatitude=0,%
Xorigine=40,%
Yorigine=70,%
Zorigine=-10}
\BouleFrame[fillstyle=solid,fillcolor=yellow](0,0)(30,-60)
\BouleQuadrillage[linecolor=blue,linewidth=0.05mm,grille=10,%
Ymin=-60,Ymax=0,Xmin=0,Xmax=30]}
% plan vertical à droite
{\psset{normaleLongitude=-90,%
normaleLatitude=0,%
Xorigine=40,%
Yorigine=-70,%
Zorigine=-10}
\BouleFrame[fillstyle=solid,fillcolor=yellow](0,0)(30,-60)
\BouleQuadrillage[linecolor=blue,linewidth=0.05mm,grille=10,%
Ymin=-60,Ymax=0,Xmin=0,Xmax=30]}
\end{pspicture}
|
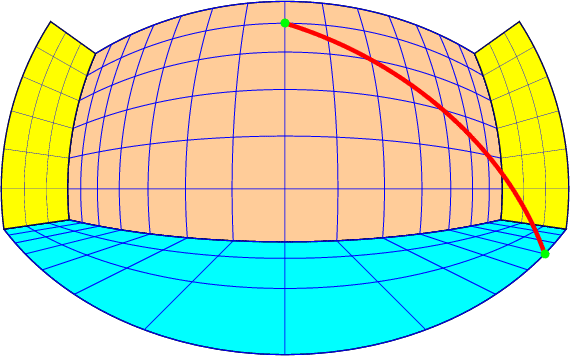
\BoulePoint(40,0,40){A}
\psdot[dotsize=1mm,linecolor=green](A)
\BoulePoint(10,-40,-10){B}
\psdot[dotsize=1mm,linecolor=green](B)
\BouleLine[linecolor=red](40,0,40)(10,-40,-10)
|
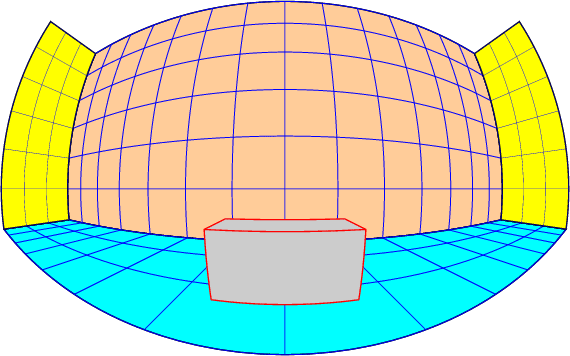
\psset{A=2.5,B=5,C=A,fillstyle=solid,fillcolor=GrisClair,linecolor=red}
\psset{CX=10,CZ=-5,CY=0}
\Cube
|

\psset{CX=15,CZ=-5,CY=0,RotZ=30}
|

\psset{A=2.5,B=A,C=A,fillstyle=solid,fillcolor=GrisClair,linecolor=red}
\psset{CX=15,CZ=-5,CY=10,RotZ=60,RotX=90}
\Die
\psset{A=5,B=A,C=A,fillstyle=solid,fillcolor=OrangeTresPale,linecolor=red}
\psset{CX=25,CZ=5,CY=-5,RotZ=45,RotY=20,RotX=-60}
\Die
|
\BouleCircle[...]{radius}
\BouleArc[...]{radius}{angle_min}{angle_max} : respectez l’ordre des angles limites sinon l’interpréteur PostScript signalera une erreur.
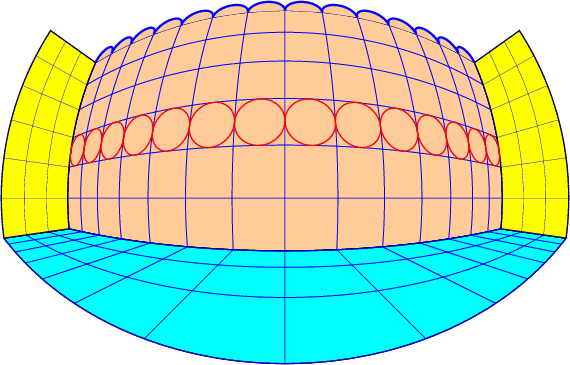
\psset{normaleLongitude=0,%
normaleLatitude=0,%
Xorigine=40}%
\multido{\iYorigine=-65+10}{14}{%
\psset{Yorigine=\iYorigine,Zorigine=15}
\BouleCircle[linecolor=red]{5}}
\multido{\iYorigine=-65+10}{14}{%
\psset{Yorigine=\iYorigine,Zorigine=50}
\BouleArc[linecolor=blue,linewidth=0.5mm,%
fillstyle=solid,fillcolor=OrangePale]{5}{180}{360}}
|

\multido{\iCY=-65+10,\iRotX=0+20}{7}{%
\psset{CY=\iCY,CZ=-5,CX=15,RotX=\iRotX}
\psset{fillstyle=gradient,gradbegin=white,gradend=red,%
gradmidpoint=0.2,linecolor=magenta,linewidth=0.05mm}
\BouleSphere{5}}
|
\BouleCylindre{radius}{hauteur}
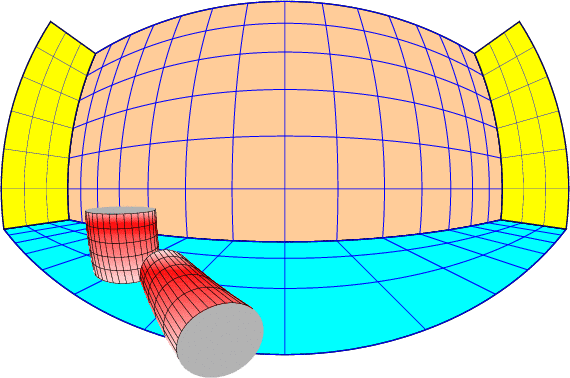
\psset{fillstyle=gradient,gradbegin=white,gradend=red,%
gradmidpoint=0.2,linewidth=0.1mm}
{\psset{CX=20,CY=20,CZ=-10}
\BouleCylindre{5}{7.5}}
{\psset{CX=15,CY=10,CZ=-7.5,RotY=90,RotX=-45}
\BouleCylindre{2.5}{-10}}
|
\BouleCone[fracHcone=0.5]{radius}{hauteur} fracHcone est obligatoirement un nombre compris entre 0 et 1.
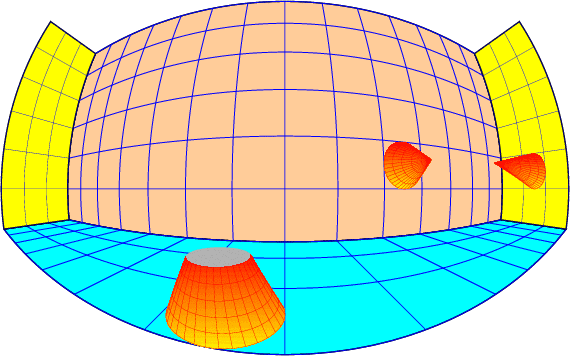
{\psset{CX=15,CZ=-10,CY=5,fracHcone=0.5}
\BouleCone{5}{10}}
{\psset{CX=40,CZ=5,CY=-25,RotY=-90}
\BouleCone{5}{10}}
{\psset{CX=25,CZ=5,CY=-70,RotX=-90}
\BouleCone{5}{30}}
|
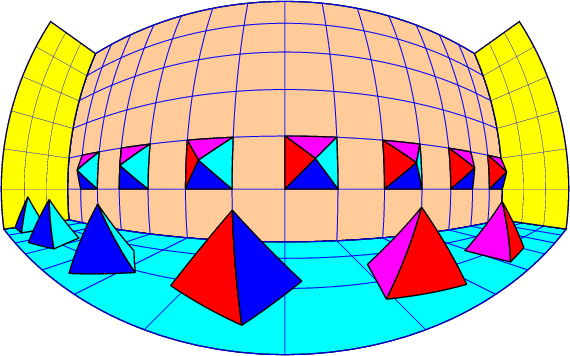
\psset{fillstyle=solid,linecolor=black,A=5}
\multido{\nY=-65+20.0}{4}{%
\psset{RotX=0,RotZ=0,RotY=-90,CX=40,CZ=5,CY=\nY,Hpyramide=5}
\Pyramide}
\multido{\nY=65+-20.0,\iRotZ=0+20}{6}{%
\psset{RotX=0,RotZ=\iRotZ,RotY=0,CX=20,CZ=-10,CY=\nY,Hpyramide=8}
\Pyramide}
|

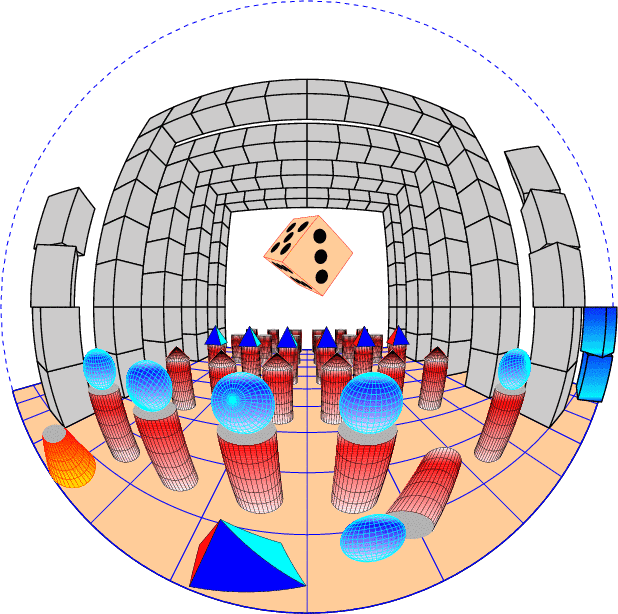
Nous pouvons maintenant nous atteler à la tâche de construire des décors en 3D vus dans une boule qui soient intéressants et artistiques, un prolongement vers une animation est toujours possible. J’ai pensé inclure dans ce package, à l’aide d’une option, la 3D conventionnelle : il suffit de changer les formules relatives à la boule et d’y rajouter les paramètres relatifs au point de vue, mais finalement cela aurait trop alourdi cette étude – vous pouvez regardez la commande \pnodeTroisD et les nombreuses applications développées dans ma page personnelle.
Une remarque importante : si le calcul des faces cachées est pris en compte pour chaque objet pris individuellement, il en est pas de même pour l’ensemble du panorama. Il convient donc de placer en premier les objets les plus éloignés de boule, puis ceux qui sont de plus en plus proche de la boule.
Si vous imaginez d’autres briques de décor, ou bien des décors étonnants, je serais heureux de le savoir.
Adapté par Manuel Luque, avec pour la mise en page LATEX, PSTricks pour les schémas et TEX-4ht pour la conversion en page HTML.
Les sources : boulemiroir.zipJe remercie Bruno Guegan pour sa relecture. Bruno lance un appel à ceux qui sont intéressés, à le rejoindre dans le projet Linux qu’il anime : Développement php et MySql : http://www.les-iles.linux-fan.com et http://www.projet.linux-fan.com.