|
1o — Deux lignes brillantes, L1 et L2 droites ou courbes, tournent rapidement dans des plans parallèles voisins ; leurs vitesses angulaires sont entre elles dans un rapport simple. L’œil placé devant le système distingue, dans l’espèce de gaze que semble produire le mouvement des lignes, l’image immobile d’une troisième courbe I plus sombre que le fond sur lequel elle se dessine. Cette courbe I est le lieu des points d’intersection apparents des lignes en mouvement.
................................................................................................
2o — À chaque instant, pour tous les points d’intersection apparente, l’œil ne reçoit de lumière que de la
ligne devant, puisqu’elle est opaque et intercepte la lumière envoyée par la ligne d’arrière. Les points
d’intersection apparaissent donc en sombre. La continuité du lieu de ces points (courbe d’intersection) est due
à la persistance des impressions lumineuses.
1o — Choisissons pour une des lignes mobiles une fente rectiligne percée dans un cercle noir. Donnons-nous la courbe d’intersection I.
[ ....................................................... C’est un nouveau genre d’anamorphoses
]
2o — VITESSES DE SENS INVERSES.
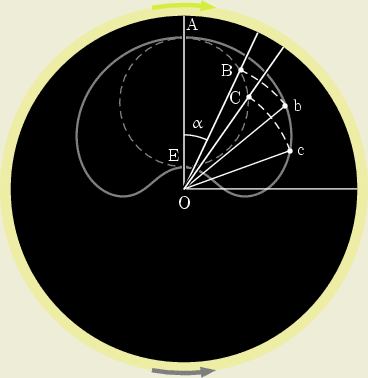
Fixons les idées par un exemple simple (fig.1).
La courbe I qu’on doit voir, est un cercle ABC. . . la fente tourne dans le sens des aiguilles d’une montre avec une vitesse constante ; le dessin Abc. . . tourne en sens inverse avec le même vitesse.
Cherchons quel doit être ce dessin.
Dans la position initiale, au temps origine, la fente est en OA. Les points du dessin sont donc A et E.
Quand la fente vient en OB, il faut que l’une de ses intersections avec le dessin soit le point B. Mais le dessin a tourné du même angle AOB en sens inverse. Donc à l’origine des temps, le point qui apparaît en B quand la fente est en OB, devait être en b tel que, le rayon restant le même, l’angle AOb soit double de AOB. Et ainsi de suite.
................................................................................................
D’une manière générale, soit V la vitesse angulaire de la fente, soit v celle du dessin déformé qui est par hypothèse de sens contraire.
Pour passer de la courbe à obtenir au dessin déformé, il faut dilater les angles dans le rapport de :
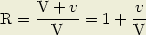
Il faut que le quotient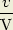 
soit un nombre entier pour que la figure soit immobile.
Le lecteur vérifiera aisément qu’à raison de la persistance des sensations lumineuses, on aperçoit simultanément R figures identiques, symétriquement distribuées autour du centre.
Si l’on veut que les dessins réguliers soient complètement séparés, il faut qu’ils occupent un angle
inférieur à 2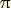
: R.
................................................................................................
1o — Le problème des courbes tournantes admet comme cas particulier la translation de l’une des courbes : c’est le problème classique de la roue passant derrière une palissade.
Comme instinctivement l’œil fixe le centre de la roue, que par suite il ne s’agit que de mouvements relatifs, nous ramenons immédiatement le problème à cet autre : Une droite lumineuse L tourne d’un mouvement uniforme autour du point fixe C : déterminer le lieu de son intersection P avec la fente F qui se déplace parallèlement à elle-même avec une vitesse constante (2).
Les équations du lieu cherché sont (avec les signes spécifiés sur la figure 2).
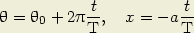
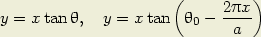
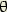0 ; il correspond donc
à des rayons différents de la roue.
L’angle 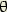0 détermine l’azimut de ces rayons quand x = 0, c’est-à-dire quand la fente mobile coïncide avec
le centre du cercle.
Le faisceau de courbes reste le même si on remplace x par x + ka : 2, où k est un nombre
entier quelconque ; l’argument de la tangente change alors d’un nombre quelconque de fois .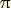
2o — La courbure apparente des rayons dépend du rapport des vitesses de translation et de rotation,
rapport mesuré par a longueur dont se déplace la fente pendant que la droite fait un tour. Dans le cas de la
roue roulant sur le sol, a = 2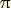R ; R est le rayon de la jante. D’où résulte que la courbure apparente des
rayons ne dépend pas de la vitesse de la roue.
[. . . ]
1o — Considérons un faisceau de courbes :
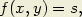
Parmi toutes ces courbes, distinguons en deux faisceaux F et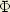 
, formés de courbes distinctes les unes des
autres :
sont des nombres entiers.
Traçons ces deux faisceaux sur du papier transparent ; à travers le papier, regardons un fond
uniformément éclairé. Nous créons ainsi un phénomène périodique, présentant ce qu’on peut appeler de
franges d’interférence. Au voisinage de certaines valeurs s1, s2, s3, du paramètre s, les courbes sont
plus resserrées ; en raison de leur épaisseur, elles se superposent plus ou moins : la lumière
transmise est donc plus grande. Au voisinage des valeurs intermédiaires du paramètre s, les courbes
sont plus uniformément réparties ; elles ne se recouvrent pas : le lumière transmise est plus
petite.
2o — Le phénomène précédent se produit, par exemple, quand on regarde normalement, deux grilles
planes identiques, à barreaux parallèles, situées dans des plans parallèles (comme deux garde-fous de pont).
 | (1) |
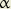et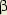 
sont des nombres peu différents ; les paramètres t et sont la suite des nombres entiers.
La figure 4 représente la superposition de deux faisceaux de droites pour 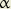= 1, 0 et 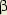= 1, 1.
On supposera aux traits une épaisseur plus grande ; on ne l’a pas donné pour rendre la figure plus intelligible.
Multiplions les nombres 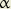et 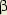par la puissance de 10n de 10 la plus petite qui les rend entiers. Il est clair
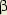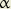que la période est t = 10n, intervalles du premier faisceau, et de de = 10n intervalles du
second.
Dans le cas de la figure, la période est de 11 intervalles du premier faisceau et de 10 du second.
3o — Le lecteur construira aisément une figure avec des cercles concentriques.
Dans l’étude des interférences (anneaux de Newton), nous trouverons réalisé le ca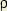s : 
= s,
avec les conditions 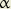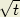: s = 
, s =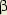 
;
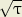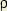est le rayon des cercles ; les paramètres t et sont la suite des nombres entiers.
Je ne reproduis pas ce paragraphe, qui traite ce sujet d’une façon générale. Le § suivant est l’illustration d’un cas particulier de moiré de seconde espèce.
1o — Considérons les deux faisceaux de droites respectivement parallèles :
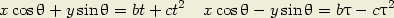 | (2) |
= 0, nous avons les deux droites OS2 et OS1; elles font évidemment le même angle 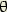avec
l’axe Oy.
Les courbes lieu des points d’intersection, qui correspondent aux petites diagonales des parallélogrammes, satisfont à la condition :
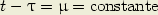
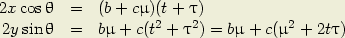
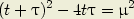
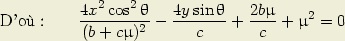 | (3) |
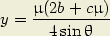 | (4) |
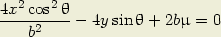
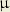glissant parallèlement Oy. Les sommets sont aux
points :
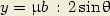 | (5) |
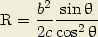
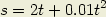
Dans la préface de son livre Cordes et membranes (1926), Henri Bouasse disserte longuement, sur le mémoire de Réaumur sur le thermomètre (1730), qu’il donne en exemple d’œuvre scientifique remarquable. Puis il entrouvre la porte pour une récréation, que je vous laisse goûter :
................................................................................................
Récemment je reçus la lettre suivante, que je crois devoir communiquer au public, bien que mon amour-propre n’ait pas lieu d’en être satisfait.
Il y a quelques semaines, sous un faux nom, je vous fis une visite pour contenter la turlutaine d’un ami sédentaire qui désire savoir si les gens ont le nez camus ou en trompette. Vous me reçûtes bien ; mais je fus choqué de vous trouver en bras de chemise, sans faux col, une cigarette à la bouche. Un tel débraillé me blessa, car je suis droguiste et notable commerçant.
Je vous trouvai au milieu de livres dont je comptai 14 grand ouverts, ce qui n’ajouta pas à mon admiration, ayant pour habitude de n’en lire qu’un à la fois (quand j’en lis).
Devant, vous s’étalait un vieil in-quarto (mon ami est libraire, 1 7, rue Lénine) que vous considériez avec amour. Ne sachant que dire, je m’enquis de ce qu’il contenait.
Ce fut comme, si j’avais ouvert la bonde d’un tonneau plein. Il s’agissait de Réaumur et des thermomètres, sujet fort convenable parce que, droguiste, je le possède dans ses grandes lignes. Monsieur, vous fûtes long, mais parvîntes à m’intéresser ; quand je vous quittai, j’avais presque oublié votre manque de tenue.
Eh bien ! Monsieur, ma première impression était la bonne : vous n’êtes qu’un fumiste ou un abruti.
Avant-hier je me trouvais dans la boutique de mon ami. Sur le comptoir j’avisai un magnifique volume que j’ouvris machinalement. Quelle ne fut pas ma stupeur de lire, à propos de Réaumur, la page que voici !
« C’est à Réaumur qu’est due la première unification des degrés thermométriques dans un travail publié en 1730 où les méthodes qu’il employait sont minutieusement décrites. Il renonce (et cela n’était pas un progrès) aux deux points fixes d’Amontons, pour ne conserver que le point de fusion de la glace où il place le zéro ; la graduation est déterminée par cette condition que pour chaque degré, le liquide (de l’esprit-de-vin) se dilate de la millième partie de son volume initial. Le thermomètre de Réaumur devint rapidement d’un usage presque universel : chose curieuse, tandis qu’il a disparu depuis longtemps en France, il s’est maintenu dans les pays de langue allemande par choix du point d’ébullition de l’eau (80o) qui conserve l’échelle de Réaumur. »
Je n’eu pas un instant de doute sur la valeur de ce texte. Le volume en question, imprimé sur beau papier et fort cher, est le tome XIV de l’ Histoire de la Nation française ; le signataire est ancien élève de l’École polytechnique, professeur à la Sorbonne, membre de l’Institut, de cet Institut que vous avez l’inconvenance d’appeler le Dépôt National des Pets-de-Loup, alors qu’il est le Panthéon de nos Gloires.
Je conclus. Vous êtes un mauvais plaisant (je crois bien avoir remarqué votre œil goguenard) ; plus vraisemblablement vous êtes gâteux. Dans ce cas Monsieur, achetez une petite voiture, installez-vous dedans qu’on vous promène au soleil, dodelinant de la tête et faisant ga, ga, ga, ga !
Vous n’avez aucun titre, aucune décoration ; vous n’appartenez à aucune société savante, vous n’avez même aucune relation avec l’Institut National de Recherches Scientifiques ou celui de Coopération Internationale Intellectuelle (si utiles : ils donnent la matérielle à deux de mes neveux, trop bêtes pour que je les garde dans mes magasins). Vous n’êtes pas riche. Et vous avez la prétention ridicule d’exister par vous-même, d’avoir des idées personnelles surtout, y compris le mémoire de Réaumur.
Rentrez en vous-même. Vous êtes un vieux petit fonctionnaire à 900 dollars, ce que refuserait mon caissier, ce que je donne à mes commis qui se décorent du titre d’ingénieur quand ils distinguent la margarine de la cassonade, ou la vanille de la cannelle !
Je signe d’un nom emprunté : la critique sincère, par conséquent utile, doit être anonyme ; le patient reçoit les coups sans pouvoir en tirer vengeance, et le critique accomplit sans danger sa tâche noble et salutaire.
Adapté par Manuel Luque, avec pour la mise en page LATEX, PSTricks pour les schémas et TEX-4ht pour la conversion en page HTML.
—
