trig_001.tex

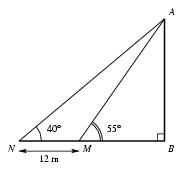
\exo {Triangle rectangle et trigonométrie}
 
{\bf Les 3~questions suivantes sont indépendantes.}
 
L'unité de longueur est le mètre.
 
Sur la figure ci-dessous, les droites $(MB)$ et $(AB)$ sont
perpendiculaires. De plus $MN = 12$, $\widehat {ANB} = 40°$ et
$\widehat {AMB} = 55°$.
\def \epspath {%
   $HOME/tex_doc/lycee/database/2nd/geometrie/triangle/}
$$
   \superboxepsillustrate {trig_001.ps}
$$
 
\itemitemalphnum Démontrer que
$$
   NB = {AB\over \tan 40°}
      \qquad \hbox {et que} \qquad
   MB = {AB\over \tan 55°}
$$
 
\itemitemalph En déduire que
$$
   AB = 12 \times {\tan 40° \times \tan 55°\over \tan 55° - \tan 40°}.
$$
 
\itemnum \` A l'aide de la calculatrice, donner une mesure de $AB$ à
un centimètre près par défaut.
 
\finexo
 
\corrige
 
\itemalphnum En utilisant $\rm tangente = opposé/adjacent$ dans les
triangles rectangles $ABN$ et $ABM$, il vient
$$
   \tan 40° = {AB\over NB}
      \quad {\rm d'où} \quad
   \dresultat {NB = {AB\over \tan 40°}}
      \qquad {\rm et} \qquad
   \tan 55° = {AB\over MB}
      \quad {\rm d'où} \quad
   \dresultat {MB = {AB\over \tan 55°}}
$$
 
\itemalph En remarquant que \dresultat {NB = 12 + MB}, il vient alors
      l'égalité
$$\eqalign {
   {AB\over \tan 40°} = 12 + {AB\over \tan 55°}
      \quad &\Longleftrightarrow \quad
   {AB\over \tan 40°} - {AB\over \tan 55°} = 12 
\cr
      &\Longleftrightarrow \quad
   AB \left( {1\over \tan 40°} - {1\over \tan 55°}\right) = 12 
\cr
      &\Longleftrightarrow \quad
   AB \left( {\tan 55° - \tan 40° \over \tan 40°\times \tan 55°}\right) = 12 
\cr
      &\Longleftrightarrow \quad
   \dresultat {
   AB = 12 \left( {\tan 40°\times \tan 55°} \over \tan 55° - \tan 40°
   \right) 
   }
\cr
}$$
 
\itemnum \` A la calculatrice, on trouve alors, à $10^{-2}$ près par
défaut, \dresultat {AB \approx 24, 41}.
 
\fincorrige