calc_013.tex

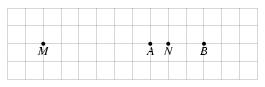
\exo {Un problème de construction}
 
Soit $A$ et $B$ deux points distincts. Placer les points $M$ et $N$
tels que
$$
   3\overrightarrow {MA} - 2\overrightarrow {MB} = \vec 0
      \qquad {\rm et} \qquad
   \overrightarrow {NA}  = - {1\over 2}\overrightarrow {NB} .
$$
Au besoin, justifier les contructions par un calcul.
 
\finexo
 
\corrige
 
On ne peut construire directement les points $M$ et $N$ puisqu'ils
apparaissent dans 2 vecteurs distincts. Privilégions le point $A$ par
exemple. Il vient~:
$$\displaylines {
   3\overrightarrow {MA} - 2\overrightarrow {MB} = \vec 0
      \quad \Longleftrightarrow \quad
   3\overrightarrow {MA} - 2(\overrightarrow {MA} + \overrightarrow {AB}) = \vec 0
      \quad \Longleftrightarrow \quad
   \overrightarrow {MA} = 2\overrightarrow {AB}
      \quad \Longleftrightarrow \quad
   \dresultat {\overrightarrow {AM} = -2\overrightarrow {AB}}
\cr
      {\rm et} \qquad
   \overrightarrow {NA}  = - {1\over 2}\overrightarrow {NB} 
      \quad \Longleftrightarrow \quad
   \overrightarrow {NA}  = - {1\over 2}(\overrightarrow {NA} + \overrightarrow {AB} )
      \quad \Longleftrightarrow \quad
   {3\over 2}\overrightarrow {NA}  = - {1\over 2}\overrightarrow {AB}
      \quad \Longleftrightarrow \quad
   \dresultat {\overrightarrow {AN}  =  {1\over 3}\overrightarrow {AB}}
\cr }
$$
\def \epspath {%
   $HOME/tex_doc/lycee/database/2nd/geometrie/vecteurs/}
$$
   \superboxepsillustrate {calc_013.ps}
$$
 
\fincorrige