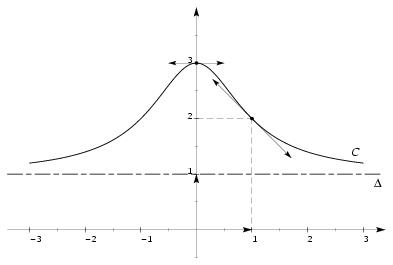
\exo {\' Etude d'une fonction rationnelle} On considère la fonction $f$ définie sur l'intervalle $[-3, 3]$ par $$ f (x) = 1 + {2\over x^2 + 1} $$ et on note $C_f$ sa courbe représentative dans le plan muni d'un repère orthonormé $(O, \vec \imath , \vec \jmath \,)$ (unité~: 2~cm ou 2~grands carreaux). \itemnum Calculer $f'$, la fonction dérivée de la fonction $f$, et vérifier qu'elle peut s'écrire sous la forme $$ f'(x) = {-4x \over \big( x^2 + 1\big) ^2} $$ \itemnum \' Etudier le signe de la dérivée $f'$ sur l'intervalle $[-3, 3]$. En déduire le tableau de variation de la fonction $f$ (en précisant les valeurs exactes des extrema). \itemnum Déterminer une équation de $T$, la tangente à la courbe $C_f$ au point d'abscisse~1. \itemnum On considère $\Delta $, la droite d'équation $y = 1$. \itemitemalph Déterminer l'intersection de la droite $\Delta $ et de la courbe $C_f$. \itemitemalph Déterminer les positions relatives de la droite $\Delta $ et de la courbe $C_f$. \itemnum Construire les droites $T$ et $\Delta $ puis la courbe $C_f$. \finexo \corrige {} \itemnum On a $$ f (x) = 1 - 2 \times {1\over x^2 + 1}. $$ En utilisant la formule $(1/u)' = -u'/u^2$, on a facilement $$ f' (x) = 0 - 2 \times {2x\over x^2 + 1} \qquad {\rm soit} \qquad \dresultat {f' (x) = {-4x \over \big( x^2 + 1\big) ^2}} $$ \itemnum On remarque tout d'abord que $x^2 + 1$ est toujours différent de $0$, puisque $$ x^2 + 1 = 0 \quad \Longleftrightarrow \quad x^2 = -1 \qquad \hbox {ce qui est impossible avec $x$ réel}. $$ \item {} De plus $\big( x^2 + 1\big) ^2$ est toujours positif (c'est un carré), la dérivée est donc du signe de $-4x$. D'où le tableau~: $$\dresultat { \vcenter {\offinterlineskip \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& -3 && 0&& 3 \cr \noalign {\hrule height 1pt } -4x && &+& 0& - \cr \noalign {\hrule height 1pt } f' (x)&& &+& 0& - \cr \noalign {\hrule height 1pt} \buucenter {$f (x)$}&& \down{$1, 2$}& \brightuuparrow & \buup {$3$}& \brightddownarrow & \down{$1, 2$} \cr }}} $$ \itemnum Pour l'équation de tangente, on utilise la formule $y = f' (a) (x-a) + f (a)$ avec $a=1$. Comme $f (1) = 2$ et $f' (1) = -1$, on trouve pour la tangente \dresultat {T~: y = -x +3}. \itemalphnum Chercher l'intersection de $C_f$ et $\Delta $ revient à résoudre l'équation $$ f (x) = 1 \quad \Longleftrightarrow \quad 1 + {2\over x^2 + 1} = 1 \quad \Longleftrightarrow \quad {2\over x^2 + 1} = 0 \quad \Longleftrightarrow \quad 2 = 0 $$ Cette dernière équation n'ayant évidemment pas de solution, on en déduit que \hfill \break \tresultat {les courbes $C_f$ et $\Delta $ ne se croisent pas}. \itemalph Pour connaître les positions relatives de $C$ et $\Delta $, il faut étudier le signe de la différence $f (x) - 1$. Or $$ f (x) - 1 = {2\over x^2 + 1} $$ est toujours positif puisque $x^2 + 1$ est la somme de 2~termes positifs. (Si l'on ne s'en aperçoit pas, on a toujours le recours de calculer le discriminant $\Delta $, de s'apercevoir qu'il est négatif, et de conclure que le polynôme $x^2 + 1$ est toujours du signe de $a$, donc ici toujours positif.) On en déduit que \tresultat {la courbe $C$ est toujours au-dessus de $\Delta $}. \def \epspath {% $HOME/tex_doc/lycee/database/1ere/sti/analyse/etudes/} \epsfxsize = 120mm \itemnum D'où le graphique ci-dessous $$ \superboxepsillustrate {frct_001.ps} $$ \fincorrige