fct_009.tex

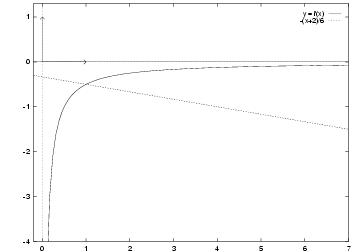
%% format               (plain.tex + fichiers de macro) OU (jpv.tex)
%% fichiers de macro    basejpv.tex
%% sujet                etude de fonction polynome
%% date                 08-01-98
%% auteur               jp vignault 
 
\exo{\'Etude d'une fonction rationnelle}
 
On considère $C_f$, la courbe représentative de la fonction $f$
définie sur $]0, 10]$ par 
$$
   f (x) = - {1 \over 2x}
$$
et $\Delta$ la droite d'équation 
$$
   y = -{1 \over 6} x -{1 \over 3}.
$$   
 
\itemnum \'Etudier les variations de la fonction $f$ (autrement dit
calculer sa dérivée $f'$, étudier le signe de cette dérivée, et dresser
le tableau des variations de $f$).
 
\itemnum Représenter, dans un même repère orthonormal, les courbes
$C_f$ et $\Delta$.%
%% \footnote{$^{(*)}$}{Si, vous avez bien lu~! $\Delta$ est bien une
%% courbe, toute droite qu'elle est\dots}
 
\itemitemalphnum Déterminer graphiquement les points d'intersection de
$C_f$ et $\Delta$.
 
\itemitemalph Retrouver ces points d'intersection par l'algèbre.
 
\itemitemalph \'Etudier les positions relatives de $C_f$ et $\Delta$.
 
\finexo
 
\corrige{}
 
\item{$\bullet$} On a \dresultat{f' (x) = {1 \over 2x^2}}, qui est évidemment
toujours strictement positive. On obtient alors le tableau de
variations (dont les limites n'étaient pas demandées) et la courbe suivante~:
 
\def \epspath{%
   $HOME/tex_doc/lycee/database/1ere/sti/analyse/fonction/}
 
\epsfxsize = 50mm
 
\def \mysmash#1{%
   \setbox \tmpbox \hbox{#1}
   \wd \tmpbox = 0pt
   \box \tmpbox}
 
$$\vcenter{
\eightpoint\rm
   \def \hfq{\hfil \ }
   \offinterlineskip
   \halign{
   % preamble
      &\hfq #\hfq
   \cr
      $x$& \vrule depth 5pt & $0$&&& $+\infty$%
   \cr
   \noalign{\hrule}
      $f' (x)$& \vrule height 10pt depth 3pt & \vrule \hskip.31em \vrule && $+$
   \cr
   \noalign{\hrule}
         \bbuucenter{$f (x)$}& \vrule& \vrule \hskip.31em \vrule & \down{$-\infty$}\hfill& 
         \bbrightuuparrow & \bbuup{$0$}% 
   \cr
}}
      \qquad
   \vcenter{\superboxepsillustrate{fct_009.ps}}
$$
 
\item{$\bullet$} Déterminer les points d'intersection de $C_f$ et
   $\Delta$ revient à résoudre le système formé par les équations des
   deux courbes.
$$\displaylines{
   \cases{
      y = - {1 \over 2x}
   \cr
      y = -{1 \over 6} x -{1 \over 3}
   \cr}
      \qquad  \Longleftrightarrow \qquad
   \cases{
      {1 \over 6} x + {1 \over 3} =  {1 \over 2x}
   \cr
      6y = -x - 2
   \cr}
      \qquad \Longleftrightarrow \qquad
   \cases{
      1 = {x^2 \over 3} + {2x \over 3} 
   \cr
      6y = -x - 2
   \cr}
\cr
       \Longleftrightarrow \qquad
   \cases{
      x^2 + 2x - 3 = 0
   \cr
      6y = -x - 2
   \cr}
      \qquad \Longleftrightarrow \qquad
   \cases{
      x = -3 \quad {\rm ou} \quad x = 1
   \cr
      6y = -x - 2
   \cr}
\cr
      \Longleftrightarrow \qquad
   (x, y) = (-3, {1\over6}) \quad {\rm ou} \quad (x, y) = (1, -{1\over2})
\cr}$$
Comme $f$ n'est pas définie pour les $x$ négatifs, on en déduit qu'il
n'y a qu'un seul point d'intersection~: \tresultat{le point $(1,
-{1\over2})$}. 
 
\item{$\bullet$} \'Etudier les positions relatives de $C_f$ et
$\Delta$ revient à étudier le signe de la différence $f (x) - (-{1
\over 6} x -{1 \over 3})$. Or on a 
$$
   f (x) - \Big( -{1 \over 6} x -{1 \over 3} \Big)
      =  {1 \over 3} (x^2 + 2x - 3)
$$
qui est du signe de $x^2 + 2x - 3$, donc négatif pour $x$ entre $-3$
et $1$, positif sinon (d'après la question précédente est en utilisant
le cours sur le signe d'un polynôme du second degré).
En conclusion 
$$
   \tresultat{$C_f$ est en dessous de $\Delta$ pour $x \in
\,]0, 1[$, en dessus sinon}.
$$
 
\fincorrige