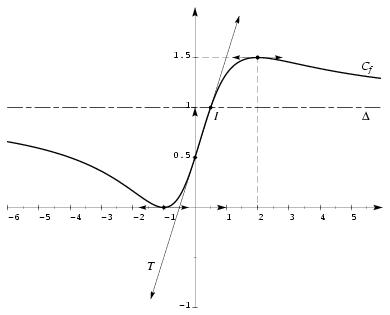
\exo {\' Etude d'une fonction rationnelle} \let \partie \centerpartie \partie {A} Soit $C$ la courbe d'équation $\displaystyle y = a + {2x + b\over x^2 + 2} $ où $a$ et $b$ sont des constantes réelles. Déterminer les nombres réels $a$ et $b$ sachant que la courbe $C$ passe par les points $A (-1; 0)$ et $\displaystyle B \left( 2; {3\over 2}\right) $. \partie {B} On considère la fonction $f$ définie pour tout $x$ de $[-6; 6]$ par $$ f (x) = {x^2 + 2x + 1 \over x^2 + 2} $$ et on note $C_f$ sa courbe représentative dans un repère orthogonal $(O, \vec u, \vec v)$. \itemnum On note $\Delta $ la droite d'équation $y = 1$. \itemitemalph Déterminer les coordonnées du point d'intersection de $C_f$ et $\Delta $. \itemitemalph \' Etudier le signe de $f (x) - 1$. En déduire les positions relatives de $C_f$ et $\Delta $. \itemitemalphnum Reproduire puis compléter le tableau de valeurs ci-dessous (on donnera des valeurs à $10^{-2}$)~près~: $$\vcenter {\offinterlineskip \def \cc#1{% \hbox to 14truemm {\hfill #1\hfill }} \halign { % preamble #\tv && \cc {$#$}& #\tv \cr \noalign {\hrule } & x&& -6&& -4&& -2&& -1&& 0&& 1&& 2&& 4&& 6& \cr \noalign {\hrule } & f (x)&& && && && && && && && && & \cr \noalign {\hrule } }} $$ \itemitemalph Ces résultat numériques sont-ils cohérents avec votre réponse du {\bf 1.}{\sl b\/})~? (Justifier.) \itemnum Calculer $f'$, la fonction dérivée de $f$, et montrer que l'on a $$ f' (x) = {2 \times \big( -x^2 + x + 2\big) \over \big( x^2 + 2\big) ^2} $$ \itemitemalphnum \' Etudier, suivant les valeurs de $x$, le signe de la fonction dérivée $f' (x)$. \itemitemalph En déduire le tableau de variation de $f$ sur l'intervalle $[-6\, ; 6]$. \itemnum Déterminer une équation de $T$, la tangente à la courbe $C_f$ au point d'abscisse~$0$. \itemnum Représenter, sur l'intervalle $[-6\, ; 6]$, la courbe $C_f$, la tangente $T$ et la droite $\Delta $. (unités graphiques~: 1~cm ou 1~grand carreau sur $Ox$, et 3~cm ou 3~grand carreaux sur $Oy$.) \finexo \corrige {} \let \partie \llappartie \partie {A} \vskip -5mm \item {} Les points $A$ et $B$ sont sur la courbe $C$, donc leurs coordonnées respectives vérifient l'équation de la courbe $C$. On a donc le système de deux équations~: $$ \cases { 0 = a + {b - 2\over 3} \cr {3\over 2} = a + {4 + b\over 4 + 2} \cr } \quad \Longrightarrow \quad \matrix { \scriptstyle (1) \cr \scriptstyle (2) \cr } \cases { 0 = 3a + b - 2 \cr 9 = 6a + 4 + b \cr } \quad \Longrightarrow \quad \matrix { \cr \scriptstyle (2) - (1) \cr } \cases { 0 = 3a + b - 2 \cr 9 = 3a + 6 \cr } \quad \Longrightarrow \quad \cases { b = -1 \cr a = 1 \cr } $$ d'où~: la courbe $C$ a pour équation \dresultat {y = 1 + {x - 1\over x^2 + 2}}. \partie {B} \vskip -5mm \itemalphnum Chercher le point d'intersection de $C_f$ et $\Delta $ revient à résoudre le système $$ \cases { y = f (x) \cr y = 1 \cr } \quad \Leftrightarrow \quad \cases { 1 = {x^2 + 2x + 1 \over x^2 + 2} \cr y = 1 \cr } \quad \Leftrightarrow \quad \cases { x^2 + 2 = x^2 + 2x + 1 \cr y = 1 \cr } \quad \Leftrightarrow \quad \cases { 1 = 2x \cr y = 1 \cr } $$ D'où l'unique point d'intersection \dresultat {I (1/ 2,1) }. \itemalph On a $$ f(x) - 1 = {x^2 + 2x + 1 \over x^2 + 2} - {x^2 + 2\over x^2 + 2} = {2x - 1 \over x^2 + 2} $$ Ce quotient est du signe de $(2x-1) \times (x^2+2)$, mais comme $x^2+2$ est toujours positif, seul intervient le signe de $2x-1$, d'où le tableau récapitulatif suivant~: $$\dresultat {\vcenter {\offinterlineskip \halign { % preamble \cc {$#$}& #\tv width 1pt & $#$ & \cc {$#$}& \cc {$#$}& \cc {$#$}& $#$ \cr x&& -\infty && 1/2 && +\infty \cr \noalign {\hrule height 1pt } 2x-1 && & - & 0& + & \cr \noalign {\hrule height 1pt } f (x) - g (x) && & - & 0 & + \cr \noalign {\hrule height 1pt } \hbox {positions relatives}& \tvi height 15pt& & \matrix {C_f {\rm \ au}\cr {\rm dessous\ de\ } \Delta }& \tv & \matrix {C_f {\rm \ au}\cr {\rm dessus\ de\ } \Delta }& \cr }}} $$ \itemalphnum On obtient $$\vcenter {\offinterlineskip \def \cc#1{% \hbox to 12.5mm {\hfill #1\hfill }} \halign { % preamble #\tv && \cc {$#$}& #\tv \cr \noalign {\hrule } & x&& -6&& -4&& -2&& -1&& 0&& 1&& 2&& 4&& 6& \cr \noalign {\hrule } & f (x)&& 0, 66&& 0, 5&& 0, 17&& 0&& 0, 5&& 1, 33&& 1, 5&& 1, 39&& 1, 29& \cr \noalign {\hrule } }} $$ \itemalph \tresultat {Les résultats sont cohérents} puisque l'on a bien $f (x) \leq 1$ pour $x< 1/2$ et $f (x) \geq 1$ pour $x> 1/2$. \itemnum On utilise la formule de dérivée d'un quotient $$ \left( {u\over v}\right) ' = {u'v - uv' \over v^2}. $$ Il vient alors $$ f' (x) = {(2x+2)(x^2+2) - 2x(x^2+2x+1) \over \left( x^2+2\right) ^2} = {-2x^2 +2x +4 \over \left( x^2+2\right) ^2} $$ On a donc bien $$\dresultat { f' (x) = {2 \times \big( -x^2 + x + 2\big) \over \big( x^2 + 2\big) ^2} }$$ \itemnum Ce quotient est du signe du produit $2 \times \big( -x^2 + x + 2\big) \times \big( x^2 + 2\big) ^2$, mais comme $2$ et $\big( x^2 + 2\big) ^2$ sont strictement positifs, seul le signe de $-x^2+x+2$ intervient. On utilise alors la méthode du discriminant $\Delta $, ici égal à $9$, pour trouver les 2~racines $$ x_1 = {-1+3\over -2} = -1 \qquad {\rm et} \qquad x_2 = {-1-3\over -2} = 2 $$ et l'on sait que le polynôme $-x^2+x+2$ est du signe de $-a$ (donc ici positif) entre les racines $x_1$ et $x_2$. D'où le tableau de variation de $f$ sur $[-6\, ; 6]$: $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& -6&& -1&& 2&& 6& \cr \noalign {\hrule height 1pt} f' (x)&& & -& 0& +& 0& - \cr \noalign {\hrule height 1pt} \buucenter {$f (x)$}&& \buup {$\approx 0, 66$}& \brightddownarrow & \down{$0$}& \brightuuparrow & \buup {$3/2$}& \brightddownarrow & \down{$\approx 1, 29$} \cr }} }$$ \itemnum En utilisant la formule $y = f' (a) (x-a) + f (a)$ avec $a=0$, il vient \dresultat {T~: y = x + {1\over 2}}. \def \epspath {% $HOME/tex_doc/lycee/database/1ere/sti/analyse/fonction/} \epsfxsize = 65mm \itemnum $$ \superboxepsillustrate {frct_002.ps} $$ \fincorrige