cerc_006.tex

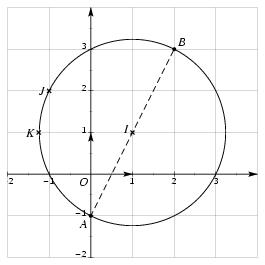
%% format               (plain.tex + fichiers de macro) OU (jpv.tex)
%% fichiers de macro    basejpv.tex
%% sujet                equation de cercle
%% date                 20-01-98
%% auteur               jp vignault 
 
\exo{\'Equations de cercles en géométrie analytique}
 
Le plan est rapporté à un repère orthonormé 
$(O, \vec \imath, \vec \jmath\/)$ (unité graphique~:
1~cm ou 1~grand carreau). 
On considère les points $A (0, -1)$ et $B (2, 3)$.
 
\itemnum Faire un dessin (que l'on complétera au fur et à 
mesure des questions).
 
\itemnum Déterminer les coordonnées de $\smash{\overrightarrow{AB}}$,
puis calculer $\Vert \smash{\overrightarrow{AB}} \Vert$, 
$\smash{\overrightarrow{AB}} \cdot \vec \imath$ 
et $\smash{\overrightarrow{AB}} \cdot \vec \jmath$.
 
\itemnum Montrer qu'une équation de $\cal C$, le cercle de diamètre 
$[AB]$ est 
$$
   x^2 - 2x + y^2 - 2y - 3 = 0.
$$
Préciser son centre $I$ et son rayon $r$.
 
\itemnum Tracer $\cal C$ sur le graphique.
 
\itemnum Les points $J (-1, 2)$ et $K (-5 /4, 1)$ sont-ils sur le
cercle $\cal C$~? (Justifier.)
 
\itemnum Déterminer les coordonnées des points
d'intersection de $\cal C$ avec 
les axes du repère.
%%% l'axe $0y$ du repère.
 
\finexo
 
\corrige{}
 
\def \epspath{%
   $HOME/tex_doc/lycee/database/1ere/sti/geometry/cercle/}
 
\epsfxsize = 60mm
 
\rightsuperboxepsillustrate{cerc_006.ps}{-13}
%
\advance \alphno by 1
%
\alph\ On trouve facilement~:
$$\displaylines{
   \dresultat{\overrightarrow{AB} = \pmatrix{2 \cr 4 \cr}},
      \qquad
   \dresultat{\Vert \overrightarrow{AB} \Vert = \sqrt{20} = 2 \sqrt5},
\cr %      \qquad
   \dresultat{\overrightarrow{AB} \cdot \vec \imath = 2},
      \qquad
   \dresultat{\overrightarrow{AB} \cdot \vec \jmath = 4}
\cr
}$$
 
\alph\ Le cercle cherché a pour centre le milieu $I$ de $[AB]$, et son
      rayon est ${1\over2} \smash{\Vert \overrightarrow{AB} \Vert}$. 
      Comme $I = ({1\over2} (x_A + x_B), {1\over2} (y_A +
      y_B))$. On a donc pour centre \mresultat{I (1, 1)} et pour rayon
      \mresultat{r = \sqrt5}. De plus il vient, pour équation de $\cal
      C$~: 
$$
   \dresultat{{\cal C}~: \quad
      (x-1)^2 + (y-1)^2 = 5}
$$
ce qui donne bien, après développement, l'équation proposée.
 
\advance \alphno by 1
 
\alph\ Le point \tresultat{$J$ est sur le cercle} car ses coordonnées
vérifient l'équation proposée. En revanche, les coordonnées de $K$ ne
vé\-ri\-fient pas cette équation, on en déduit que \tresultat{$K$ n'est
pas sur $\cal C$}.
 
\alph\ $\bullet$ {\sl Intersection de $\cal C$ avec l'axe $Oy$\/}~:
      il suffit de résoudre le système      
$$
   \cases{
      x = 0
   \cr
      x^2 - 2x + y^2 - 2y - 3 = 0
   \cr}
      \qquad \Longleftrightarrow \qquad
   \cases{
      x = 0
   \cr
      y^2 - 2y - 3 = 0
   \cr}
      \qquad \Longleftrightarrow \qquad
   \cases{
      x = 0
   \cr
      y = 3 \quad {\rm ou} \quad y = -1
   \cr}
$$
La dernière équivalence provenant du fait que 
l'équation $y^2 - 2y - 3 = 0$ admet deux solutions $y_1$ et $y_2$
puisque le discriminant $\Delta$ est positif (on trouve $\Delta = 16 =
4^2$). 
 
Il n'a donc deux points d'intersection avec l'axe $Oy$~:
\tresultat{les point $(0, -1)$ et $(0, 3)$}.
 
$\bullet$ {\sl Intersection de $\cal C$ avec l'axe $Ox$\/}~:
      il suffit de résoudre le système      
$$
   \cases{
      y = 0
   \cr
      x^2 - 2x + y^2 - 2y - 3 = 0
   \cr}
      \qquad \Longleftrightarrow \qquad
   \cases{
      y = 0
   \cr
      x^2 - 2x - 3 = 0
   \cr}
      \qquad \Longleftrightarrow \qquad
   \cases{
      y = 0
   \cr
      x = 3 \quad {\rm ou} \quad x = -1
   \cr}
$$
Il n'a donc deux points d'intersection avec l'axe $Ox$~:
\tresultat{les points $(-1, 0)$ et $(3, 0)$}.
 
 
 
\fincorrige