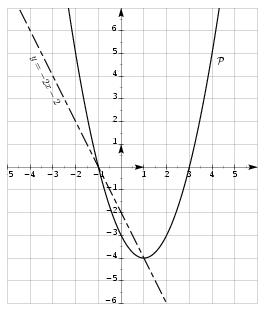
\exo {\' Etude de fonction, résolution graphique d'équation} La fonction $f$ est définie sur $\rset $ par $f (x) = x^2 -2x -3$. On appelle $\cal P$ la courbe qui représente $f$ dans un repère orthonormal d'origine $O$ (unité graphique~: 1~cm ou 1~grand carreau). \itemnum Vérifier que~: \quad $f (x) = (x - 1)^2 - 4$. \itemnum Démontrer que la fonction $f$ est croissante sur $[1; +\infty [$. \item {} On admet que $f$ est décroissante sur $]-\infty ; 1]$ (ne pas le démontrer). \itemnum \' Etablir le tableau de variations de $f$. \itemnum Calculer les coordonnées des points d'intersection de $\cal P$ avec les axes de coordonnées. \itemitemalphnum Compléter le tableau de valeurs suivant~: $$\vcenter {\offinterlineskip \def \cc#1{% \hbox to 12mm {\hfill #1\hfill }} \halign { % preamble #\tv && \cc {$#$}& #\tv \cr \noalign {\hrule } & x&& -2&& -1&& 0&& 0, 5&& 1&& 1, 5&& 2&& 3&& 4& \cr \noalign {\hrule } & f (x)&& && && && && && && && && & \cr \noalign {\hrule } }} $$ \itemitemalph Tracer la courbe $\cal P$. \itemnum Résoudre graphiquement l'inéquation ~: \quad $f (x) > -3$. \itemnum Résoudre par le calcul l'inéquation~: \quad $f (x) \geq 0$. \itemitemalphnum Résoudre par le calcul l'inéquation~: \quad $f (x) = -2x - 2$. \itemitemalph Comment résoudre graphiquement cette dernière équation~? \finexo \corrige \itemnum Il est clair que l'on a \dresultat {f (x) = (x-1)^2 -4} puisque $(x-1)^2 = x^2 - 2x +1$. \itemnum Soit $a$ et $b$ deux nombres réels vérifiant $1 \leq a \leq b$. Il nous faut montrer que $f (a) \leq f (b)$. Or $$\eqalign { 1\leq a\leq b \quad &\Longrightarrow \quad 0\leq a-1\leq b-1 \cr &\Longrightarrow \quad 0\leq (a-1)^2\leq (b-1)^2 \cr &\Longrightarrow \quad -4\leq (a-1)^2 -4\leq (b-1)^2 -4 \quad \Longrightarrow \quad -4\leq f (a)\leq f (b) \cr }$$ Ce qui prouve que \tresultat {$f$ est croissante sur $[1; +\infty [$}. \itemnum D'où le tableau de variation de $f$~: $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& -\infty && 1&& +\infty \cr \noalign {\hrule } \buucenter {$f (x)$}&& & \brightddownarrow & \down {$-3$}& \brightuuparrow & \buup {\phantom {1}} \cr }} }$$ \itemnum Chercher l'intersection de $\cal P$ avec l'axe $Oy$ revient à résoudre le système $$ \cases { x = 0 \cr y = f (x) \cr } \quad \Longrightarrow \quad \cases { x = 0 \cr y = f (0) = -3 \cr } \quad \tresultat {d'où l'unique point d'intersection~: $(0; -3)$.} $$ \item {} De la même façon, chercher l'intersection de $\cal P$ avec l'axe $Ox$ revient à résoudre le système $$ \cases { y = 0 \cr y = f (x) \cr } \quad \Longrightarrow \quad \cases { y = 0 \cr 0 = (x-1)^2 - 4 \cr } \quad \Longrightarrow \quad \cases { y = 0 \cr 0 = (x-3) (x+1) \cr } \quad \Longrightarrow \quad \cases { y = 0 \cr x=3& ou $x=-1$ \cr } $$ d'où les \tresultat {deux points d'intersection~: $(3; 0)$ et $(-1; 0)$}. \itemnum $$\vcenter {\offinterlineskip \def \cc#1{% \hbox to 14mm {\hfill #1\hfill }} \halign { % preamble #\tv && \cc {$#$}& #\tv \cr \noalign {\hrule } & x&& -2&& -1&& 0&& 0, 5&& 1&& 1, 5&& 2&& 3&& 4& \cr \noalign {\hrule } & f (x)&& 5&& 0&& -3&& -3, 75&& -4&& -3, 75&& -3&& 0&& 5& \cr \noalign {\hrule } }} $$ % \def \epspath {% $HOME/tex_doc/lycee/database/2nd/analyse/fonctions/} $$ \superboxepsillustrate {synt_001.ps} $$ \itemnum Graphiquement, les solutions de l'inéquation $f (x)> -3$ sont \tresultat {tous les nombres de $]-\infty ;0[\, \cup \, ]2;+\infty [$}. \itemnum Il vient $$ f (x) \geq 0 \quad \Longleftrightarrow \quad (x-1)^2 - 4 \geq 0 \quad \Longleftrightarrow \quad (x-1)^2 - 2^2 \geq 0 \quad \Longleftrightarrow \quad (x-3) (x+1) \geq 0 $$ Le tableau de signes s'impose, et il vient $$\vcenter {\offinterlineskip \eightpoint \rm \halign { % preamble #& \cc {$#$}& \tv #& $#$& \cc {$#$} & \cc {$#$} & \cc {$#$} & \cc {$#$} & \cc {$#$} & $#$ \cr & x && -\infty && -1 && 3 &&+\infty \cr \noalign {\hrule height 1pt} & x-3 &&& - & \tv & - & 0 & + \cr \noalign {\hrule } & x+1 &&& - & 0 & + & \tv & + \cr \noalign {\hrule height 1pt} & \rm produit &&& + & 0 & - & 0 & + \cr }}$$ d'où l'ensemble des solutions~: \dresultat {S = \, ]-\infty ; -1]\cup [3; +\infty [} \itemnum Il vient $$ f (x) = -2x -2 \quad \Longleftrightarrow \quad x^2 - 2x - 3 = -2x - 2 \quad \Longleftrightarrow \quad x^2 - 1 = 0 \quad \Longleftrightarrow \quad (x - 1) (x+1) = 0 $$ D'où les deux solutions~: \tresultat {$x=1$ et $x= -1$}. \item {} Graphiquement, résoudre cette équation revient à rechercher $$ \tresultat {les abscisses des points d'intersection de la courbe $\cal P$ avec la droite d'équation $y = -2x-2$}. $$ \fincorrige