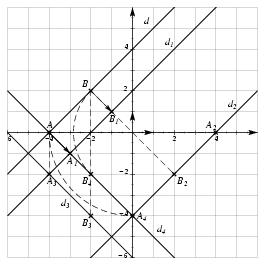
\exo {Transformations usuelles} Dans le plan rapporté à un repère orthonormal $(O, \vec \imath , \vec \jmath \,)$, on considère les points $$ A (-4; 0) \qquad {\rm et} \qquad B (-2; 2), $$ et on nomme $d$ la droite$(AB)$. \itemnum On considère $t$, la translation de vecteur $\vec u {1\choose -1}$, et on nomme $d_1$ l'image de la droite $d$ par cette translation. \itemitemalph Sur un graphique, représenter la droite $d$ et son image $d_1$. \itemitemalph Déterminer, par le calcul, l'image $A_1$ du point $A$ par cette translation. \itemitemalph Déterminer, par le calcul, l'image $B_1$ du point $B$ par cette translation. \itemitemalph En déduire une équation de $d_1$. \itemnum On considère $s$, la symétrie centrale de centre $O$, et on nomme $d_2$ l'image de la droite $d$ par cette symétrie. \itemitemalph Représenter $d_2$ sur le graphique précédent. \itemitemalph Déterminer, par le calcul, une équation de $d_2$. \itemnum On considère $\cal S$, la symétrie axiale d'axe la droite d'équation $y = -1$, et on nomme $d_3$ l'image de la droite $d$ par cette symétrie. \itemitemalph Représenter $d_3$ sur le graphique précédent. \itemitemalph Lire sur le graphique une équation de $d_3$ (aucune justification n'est demandée). \itemnum On considère $r$, la rotation de centre $O$ et d'angle $\pi /2$, et on nomme $d_4$ l'image de la droite $d$ par cette rotation. \item {} Représenter $d_4$ sur le graphique précédent. \finexo \corrige \itemalphnum \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/transform/} $$ \superboxepsillustrate {synt_001.ps} $$ \itemalph Par définition de la translation, on a $\overrightarrow {AA_1} = \vec u$. Ce qui donne~: $$ \overrightarrow {AA_1} = \vec u \quad \Longleftrightarrow \quad {x_1 + 4\choose y_1} = {1\choose -1} \quad \Longleftrightarrow \quad \cases { x_1 + 4 = 1 \cr y_1 = -1 \cr } \qquad {\rm d'où} \qquad \dresultat {A_1 (-3 ; -1)}. $$ \itemalph De la même façon, il vient $$ \overrightarrow {BB_1} = \vec u \quad \Longleftrightarrow \quad {x_1 + 2\choose y_1 - 2} = {1\choose -1} \quad \Longleftrightarrow \quad \cases { x_1 + 2 = 1 \cr y_1 - 2 = -1 \cr } \qquad {\rm d'où} \qquad \dresultat {B_1 (-1 ; 1)}. $$ \itemalph Cherchons l'équation réduite de $d_1$. Il vient $$ \overrightarrow {A_1B_1} = {2\choose 2} \qquad \hbox {donc le coefficient directeur de $d_1$ est } {2\over 2} = 1 $$ donc l'équation de $d_1$ est de la forme $y = x + b_1$. En utilisant les coordonnées du point $B_1$, on trouve facilement $b_1 = 2$, d'où l'équation cherchée \dresultat {d_1~: y = x + 2}. \itemnum \advance \alphno by 1 \alph \ Cherchons les coordonnées du points $A_2$, image du point $A$ par la symétrie $s$. Il vient $$ \overrightarrow {OA_2} = - \overrightarrow {OA} \quad \Longleftrightarrow \quad {x_2\choose y_2} = - {-4 \choose 0} \qquad {\rm d'où} \qquad \dresultat {A_2 (4; 0)} $$ Et comme l'on sait que $d_2$ est une droite parallèle à $d$, qui est elle-même parallèle à $d_1$, on en déduit que $d_2$ et $d_1$ ont le même coefficient directeur. En utilisant ensuite les coordonnées du point $A_2$, on trouve \dresultat {d_2~: y = x - 4}. \itemnum \advance \alphno by 1 \alph \ On lit \dresultat {d_3~: y = -x - 6}. \fincorrige