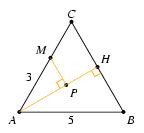
\exo {Des triangles rectangles\dots } On considère le triangle équilatéral $ABC$ de côté $5\cm $. On note $H$ le projeté orthogonal de $A$ sur $[BC]$, $M$ le point de $[AC]$ tel que $AM = 3\cm $, et $P$ le projeté orthogonal de $M$ sur $[AH]$. \def \epspath {% $HOME/tex_doc/lycee/database/2nd/geometrie/triangle/} $$ \superboxepsillustrate {rect_003.ps} $$ Calculer $AP$. ({\sl Indication~:} on pourra auparavant calculer $AH$.) \finexo \corrige {} \item {$\bullet $} Dans un triangle équilatéral, hauteur et médiatrice sont confondues, donc \tresultat {$H$ est le milieu de $[BC]$}, et \dresultat {BH = {5\over 2}}. \item {$\bullet $} On applique maintenant Pythagore dans le triangle rectangle $ABH$. Il vient $$\eqalign { AB^2 = AH^2 + BH^2 \quad &\Longrightarrow \quad 5^2 = AH^2 + \left( {5\over 2}\right) ^2 \quad \Longrightarrow \quad AH^2 = {100 - 25\over 4} = {75\over 4} \cr \quad &\Longrightarrow \quad AH = {\sqrt {3\times 5^2} \over 2} \qquad {\rm soit} \qquad \dresultat {AH = {5\sqrt 3 \over 2}} }$$ \item {$\bullet $} Ne reste plus qu'à appliquer Thalès dans le triangle $ACH$ avec le segment $[MP]$ (c'est possible puisque les droites $(MP)$ et $(HC)$ sont parallèles, car toutes~$2$ perpendiculaires à la même droite $(AH)$). \item {} Il vient alors $$ {AM\over AC} = {AP\over AH} \quad \Longrightarrow \quad {3\over 5} = {AP\over AH} \quad \Longrightarrow \quad AH \times {3\over 5} = AP \qquad {\rm soit} \qquad \dresultat {AP = {3\sqrt 3 \over 2}}. $$ \fincorrige