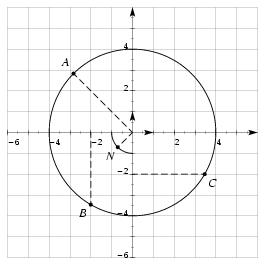
%% format (plain.tex + fichiers de macro) OU (jpv.tex) %% fichiers de macro basejpv.tex %% niveau bts mai %% genre nombres complexes %% sujet calcul sous forme trigo %% date 01-10-97 %% auteur jp vignault \exo {Forme exponentielle d'un nombre complexe} On considère les nombres complexes $$ a = -2\sqrt2 + 2i\sqrt2, \qquad b = -2 -2i\sqrt3, \qquad c = 2\sqrt3 - 2i. $$ On appelle $A$, $B$ et $C$ leurs images respectives dans le plan muni d'un repère orthonormal $(O, \vec u, \vec v\,)$. \itemitemalphnum Calculer les modules de $a$, $b$ et $c$. \itemitemalph En déduire que les points $A$, $B$ et $C$ sont tous sur un même cercle $\cal C$ dont on précisera le centre et le rayon. \itemnum Donner un argument de chacun des nombres $a$, $b$ et $c$. \itemnum Déterminer la forme exponentielle, puis la forme algébrique, du nombre complexe $$ Z = {a^3 \times b^3 \over c^6}. $$ \item{} Montrer que $Z^4 = -1$. \itemnum On appelle $N$ le point image de $Z$. Représenter $A$, $B$, $C$, $N$ et $\cal C$ dans le repère donné. On prendra 1~cm (ou un grand carreau) pour unité. \finexo \corrige \itemalphnum On trouve \tresultat{$|a| = |b| = |c| = 4$}. On en déduit l'égalité de distances $OA = OB = OC = 4$. \itemalph Les points $A$, $B$, et $C$ sont donc tous sur le même cercle $\cal C$ de centre $O$ et de rayon~4. \itemnum Pour les calculs d'argument, on trouve $$\displaylines{ \cases{ \cos \theta_a = -\sqrt2/2 \cr \sin \theta_a = \sqrt2/2 \cr} \Rightarrow \tresultat{$\theta_a = {3\pi\over4} + 2k\pi$}, \qquad \cases{ \cos \theta_b = -1/2 \cr \sin \theta_b = -\sqrt3/2 \cr} \Rightarrow \tresultat{$\theta_b = -{2\pi\over3} + 2k\pi$} \cr \cases{ \cos \theta_c = \sqrt3/2 \cr \sin \theta_c = -1/2 \cr} \Rightarrow \tresultat{$\theta_c = -{\pi\over6} + 2k\pi$} \cr }$$ Finalement, $$ \dresultat {a = \left[ 4, {3\pi\over4} \right] = 4 e^{3i\pi /4}}, \qquad \dresultat { b = \left[ 4, -{2i\pi\over3} \right] = 4 e^{-{2i\pi /3}}}, \qquad \dresultat { c = \left[ 4, -{\pi\over6} \right] = 4 e^{-{i\pi /6}}}. $$ \itemnum En calculant maintenant $Z$ avec les formules de calcul sous forme exponentielle, il vient $$ Z = {a^3 \times b^3 \over c^6} = {\left[ 4^3, {9\pi\over4} \right] \times \left[ 4^3, -2\pi\right] \over \left[ 4^6, -\pi\right]} = \left[1, {9\pi\over4} + \pi \right] = \dresultat {\left[ 1, {5\pi\over4}\right] = Z} $$ Finalement, $Z = \cos \left( 5\pi\over4\right) + i \sin \left( 5\pi\over4\right)$, soit \dresultat {Z = -{\sqrt2\over2} - i{\sqrt2\over2}} \item{} Et on a bien $Z^4 = \left[ 1, 5\pi\right] = \left[ 1, \pi\right] = e^{i\pi }$. Autrement dit, \tresultat{$Z^4 = -1$} \def \epspath {% $HOME/tex_doc/lycee/database/term/sti/algebre/complex/} \epsfxsize 80mm \itemnum $$ \superboxepsillustrate {cplx_003.ps} $$ \fincorrige