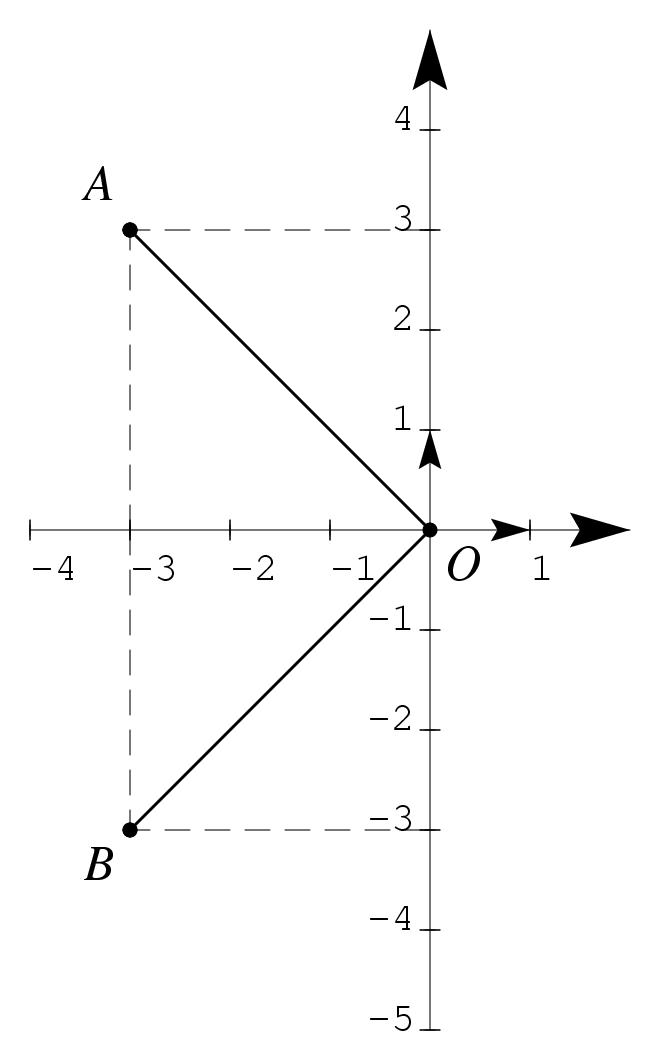
\exo {Complexes, {\sl d'après bac sti gt, juin 98\/}} Le plan est rapporté à un repère orthonormal $(O, \vec u, \vec v)$. \itemnum Résoudre dans $\cset $ l'équation~: $$ z^2 + 6z + 18 = 0. $$ \itemnum On note respectivement $A$ et $B$ les points d'affixes respectives $$ z_1 = -3 + 3i \qquad {\rm et} \qquad z_2 = -3 - 3i. $$ \itemitemalphnum Déterminer Le module et un argument de $z_1$ et $z_2$. \' Ecrire $z_1$ et $z_2$ sous forme exponentielle. \itemitemalph Représenter les points $A$ et $B$ dans le plan. \itemitemalph Montrer que le triangle $OAB$ est rectangle isocèle. \itemnum On appelle $C$ le point d'affixe $z_3 = -1 + i\sqrt 3$. \itemitemalph Déterminer le module et un argument de $z_3$. En déduire la forme trigonométrique du produit $z_1 \times z_3$. \itemitemalph Déterminer la forme algébrique du produit $z_1 \times z_3$. \itemitemalph Déduire des questions précédentes les valeurs exactes de $$ \cos \Big( {17\pi \over 12}\Big) \qquad {\rm et} \qquad \sin \Big( {17\pi \over 12}\Big) . $$ \itemitemalphnum Déterminer l'affixe du point $D$ tel que $ABDC$ soit un parallélogramme. \itemitemalph Représenter les points $C$ et $D$ dans le repère précédent. \finexo \corrige {} \def \epspath{% $HOME/tex_doc/lycee/database/term/sti/algebre/complex/} \epsfxsize = 50mm \rightsuperboxepsillustrate {exo_010.ps}{-24} % \num\ On résoud en utilisant la méthode du discriminant. On trouve $\Delta = -36$, d'où les 2~racines complexes conjuguées~: $$ \dresultat {z_1 = -3+3i} \qquad {\rm et} \qquad \dresultat {z_2 = -3-3i}. $$ %% On a $z_1 = -3 + 3i$ et $z_2 = -3-3i$. Il suffit alors de vérifier %% que $(z-z_1) (z-z_2) = z^2 + 6z + 18$, pour prouver que %% $$ %% \tresultat{$z_1$ et $z_2$ sont les 2~racines de l'équation %% $z^2 + 6z + 18 = 0$}. %% $$ \alphnum \ \alph\ On a $$ z_1 = 3\sqrt2 \left( - {\sqrt2 \over2} + i{\sqrt2 \over2}\right) \qquad {\rm et} \qquad z_2 = 3\sqrt2 \left( - {\sqrt2 \over2} - i{\sqrt2 \over2}\right). $$ D'où les résultats demandés~: $$ \mresultat{|z_1| = |z_2| =3\sqrt2} \qquad {\rm et} \qquad \mresultat{\theta_1 = 3\pi/4}, \qquad \mresultat{\theta_2 = -3\pi/4} $$ Et on a les formes exponentielles $$ \dresultat{z_1 = 3\sqrt2 \, e^{3i\pi/4}} \qquad {\rm et} \qquad \dresultat{z_2 = 3\sqrt2 \, e^{-3i\pi/4}} $$ \alph \ Connaissant les affixes de $A$ et $B$, on en déduit les coordonnées des vecteurs $\overrightarrow {OA}$ et $\overrightarrow {OB}$~: $$ \overrightarrow {OA} = \pmatrix {-3\cr 3\cr } \qquad {\rm et} \qquad \overrightarrow {OB} = \pmatrix {-3\cr -3\cr } $$ d'où le produit scalaire $$ \overrightarrow {OA} \cdot \overrightarrow {OB} = -3\times 3 -3\times (-3 = 0) $$ ce qui prouve que \tresultat {$AOB$ rectangle en $O$}. De plus, on a vu que les modules $|z_A|$ et $|z_B|$ son égaux, ce qui prouve que les distances $OA$ et $OB$ sont égales. Le triangle $AOB$ est donc également \tresultat {isocèle}. %% Comme $z_2 = z_1 \times i$, c'est à dire $z_2 = z_1 %% \times e^{i\pi/2}$, on peut affirmer, d'après le cours, que %% $$ %% \tresultat{$B$ est l'image de $A$ par la rotation de centre $O$ et %% d'angle $\pi/2$}. %% $$ \num\ Soit $z_3 = -1 + i\sqrt3$. \alph\ On trouve $$ \mresultat{|z_3| = 2}, \quad {\rm et} \quad \mresultat{\theta_3 = 2\pi/3} \qquad {\rm d'où} \qquad \mresultat{|z_1 \times z_3| = 6\sqrt2} \quad {\rm et} \quad \dresultat{{\rm Arg} (z_1 \times z_3) = {17\pi \over12}}, $$ puisque $|z_1 \cdot z_3| = |z_1| \times |z_3|$ et ${\rm Arg} (z_1 \cdot z_3) = {\rm Arg} (z_1) + {\rm Arg} (z_3)$. On a donc finalement $$ \dresultat{z_1 \cdot z_3 = \left[ 6\sqrt2, {17\pi \over12}\right] = 6\sqrt2 \left( \cos {17\pi \over12} + i \sin {17\pi \over12} \right) .} $$ \alph\ En utilisant maintenant les formes algébriques de $z_1$ et $z_3$, il vient $$ (-3+3i) (-1+i\sqrt3) = 3(1-\sqrt3) - 3i (1+\sqrt3) \qquad {\rm d'où} \qquad \mresultat{z_1 \cdot z_3 = 3(1-\sqrt3) - 3i (1+\sqrt3)} $$ \alph\ Reste à utiliser les deux relations précédentes en identifiant les parties réelles et imaginaires pour obtenir~: $$ \dresultat{\cos {17\pi \over12} = {1-\sqrt3 \over 2\sqrt2}} \qquad {\rm et} \qquad \dresultat{\sin {17\pi \over12} = {-1-\sqrt3 \over 2\sqrt2}} $$ \itemalphnum Le quadrilatère $ABDC$ est un parallélogramme si et seulement si $$\eqalign { \overrightarrow {AB} = \overrightarrow {CD} \quad &\Longleftrightarrow \quad z_B - z_A = z_D - z_C \quad \Longleftrightarrow \quad z_B - z_A + z_C = z_D \cr &\Longleftrightarrow \quad z_D = (-3 - 3i) - (-3+3i) + (-1 + i \sqrt 3) \qquad {\rm soit} \qquad \dresultat {z_D = -1 + (\sqrt3 - 6)i} }$$ \fincorrige