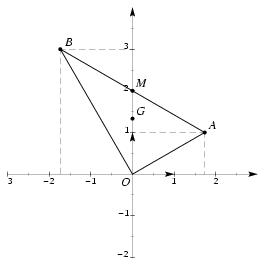
\exo {\sl ex 81 p 44, Dimathème Term Sti/Stl, éditions Didier 1997} \finexo \corrige \itemnum On a $$ z_1 = \sqrt3 + i, \qquad \qquad z_2 = -\sqrt3 + 3i, \qquad {\rm et} \qquad z_3 = {4 \sqrt3 z_2 \over 9z_1} $$ \itemalph On trouve tout d'abord \mresultat{|z_1| = 2} et \mresultat{|z_2| = 2\sqrt3}. D'où $$ \cases{ \cos \theta_1 = \sqrt3 / 2 \cr \sin \theta_1 = 1/2 \cr} \quad \Longrightarrow \quad \dresultat{\theta_1 = \pi/6} \qquad {\rm et} \qquad \cases{ \cos \theta_2 = -1/2 \cr \sin \theta_2 = \sqrt3/2 \cr} \quad \Longrightarrow \quad \dresultat{\theta_2 = 2\pi/3} $$ \itemalph En utilisant les formes trigonométriques, on obtient alors pour $z_3$ $$ z_3 = {[4\sqrt3, 0] \times [2\sqrt3, 2\pi/3] \over [9, 0] \times [2, \pi/6]} = {[24, 2\pi/3] \over [18, \pi/6]} = \left[ {4 \over3}, {2\pi \over3} - {\pi \over6} \right] = \left[ {4 \over3}, {\pi \over 2} \right] $$ d'où \dresultat{|z_3| = {4 \over3}} et \dresultat{\theta_3 = {\pi \over 2}}. La forme algébrique de $z_3$ est donc $z_3 = 4i/3$. \def \epspath{% $HOME/tex_doc/lycee/database/term/sti/algebre/complex/} \epsfxsize = 80mm \itemalphnum Visiblement, le dessin doit se faire avec des valeurs approchées. $$ \superboxepsillustrate {geom_003.ps} $$ \itemalph Calculons le produit scalaire de $\overrightarrow {OA}$ par $\overrightarrow {OB}$. On a $$ \overrightarrow{OA} = {\sqrt3 \choose 1}, \qquad \overrightarrow{OB} = {-\sqrt3 \choose 3}, \qquad {\rm donc} \qquad \overrightarrow{OA} \cdot \overrightarrow{OB} = \sqrt3 \times (-\sqrt3) + 1\times 3 = 0. $$ Les vecteurs $\overrightarrow{OA}$ et $\overrightarrow{OB}$ sont donc orthogonaux et \tresultat{le triangle $OAB$ est rectangle en $O$} \item {} {\bf autre méthode~:} On connaît déjà $OA = |z_1| = 2$ et $OB = |z_2| = 2\sqrt 3$. Ne reste plus qu'à calculer $AB = |z_2 - z_1| = |-2\sqrt 3 + 2i| = 4$, pour pouvoir appliquer Pythagore et conclure. \itemalph Le milieu du segment $[AB]$ est le point $M$ d'affixe $$ z_M = {1\over2} (z_1 + z_2) = \dresultat {2i = z_M} $$ \itemalph On connaît les affixes des vecteurs $\overrightarrow {OM}$ et $\overrightarrow {OG}$~: $$ z_{\overrightarrow {\scriptstyle OM}} = 2i \qquad {\rm et} \qquad z_{\overrightarrow {\scriptstyle OG}} = {4\over 3}i. $$ On vérifie alors facilement que $$ z_{\overrightarrow {\scriptstyle OG}} = {2\over 3} z_{\overrightarrow {\scriptstyle OM}} \qquad \hbox {ce qui prouve que} \qquad \overrightarrow {OG} = {2\over 3} \overrightarrow {OM} $$ Comme $M$ est le milieu de $[AB]$, on a donc bien \tresultat {$G$ centre de gravité de $OAB$} (car situé aux deux tiers de la médiane.) \fincorrige