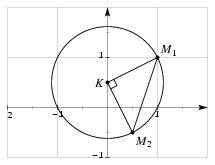
\exo {Géométrie, équation du second degré} Le nombre complexe $i$ est le nombre complexe de module $1$ et dont un argument est $\pi /2$. Le plan rapporté au repère orthonormal direct $(O, \vec u, \vec v)$ d'unité graphique $4\cm $ est noté $\cal P$. Les nombres complexes $$ 1+i, \qquad \qquad {1\over 2} - {i\over 2} \qquad {\rm et}\qquad {i\over 2} $$ sont respectivement notés $z_1$, $z_2$ et $z_3$. Les points $M_1$, $M_2$ et $K$ du plan $\cal P$ sont les points d'affixes respectives $z_1$, $z_2$ et $z_3$. \itemnum Placer les points $M_1$, $M_2$ et $K$ dans le plan $\cal P$. \itemnum Déterminer le module et l'un des arguments de chacun des nombres complexes $z_1$ et $z_2$. \itemnum Montrer que les points $M_1$ et $M_2$ sont sur un cercle de centre $K$ dont on déterminera le rayon. \item {} Tracer ce cercle dans le plan $\cal P$. \itemnum Démontrer que le triangle $M_1KM_2$ est rectangle. \itemnum Résoudre dans $\cset $ l'équation d'inconnue $z$ $$ z^2 - {1\over 2} z + {1\over 8} = 0. $$ Vérifier que le nombre complexe $\displaystyle { {z_3\over z_1} }$ est l'une des solutions de cette équation. \finexo \corrige \catcode `\|=12 \itemnum \def \epspath {% $HOME/tex_doc/lycee/database/term/sti/algebre/complex/} $$ \superboxepsillustrate {synt_001.ps} $$ \itemnum Il vient $$ \dresultat {|z_1| = \sqrt 2} \qquad {\rm d'où} \qquad \cases { \cos \theta _1 = 1/\sqrt 2 = (\sqrt 2) /2 \cr \sin \theta _1 = 1/\sqrt 2 = (\sqrt 2) /2 \cr } \quad \Longrightarrow \dresultat {\theta _1 = {\pi \over 4} \quad {\rm convient}} $$ et, de la même façon $$ \dresultat {|z_2| = {1\over \sqrt 2}} \qquad {\rm d'où} \qquad \cases { \cos \theta _2 = (\sqrt 2) /2 \cr \sin \theta _2 = - (\sqrt 2) /2 \cr } \quad \Longrightarrow \dresultat {\theta _2 = -{\pi \over 4} \quad {\rm convient}} $$ \itemnum Calculons les distances $M_1K$ et $M_2K$. Il vient $$\displaylines { M_1K = |z_3 - z_1| = \left| {i\over 2} - 1 - i\right| = \left| -1 - {1\over 2} i\right| \qquad {\rm soit} \qquad \dresultat {M_1K = \sqrt {5\over 4}} \cr {\rm et} \qquad M_2K = |z_3 - z_2| = \left| {i\over 2} - {1\over 2} + {i\over 2}\right| = \left| - {1\over 2} + i\right| \qquad {\rm soit} \qquad \dresultat {M_2K = \sqrt {5\over 4}} \cr }$$ ce qui prouve que \tresultat {$M_1$ et $M_2$ sont sur un même cercle de centre $K$ et de rayon $(\sqrt 5)/2$}. \itemnum Comme $$ M_1M_2 = |z_2 - z_1| = \left| - {1\over 2} - {3\over 2} i\right| \qquad \hbox {il vient} \qquad \dresultat {M_1M_2 = \sqrt {10\over 4}} $$ et la relation de Pythagore nous prouve que \tresultat {$M_1KM_2$ rectangle en $K$}. \itemnum Pour résoudre l'équation proposée, on utilise la méthode du discriminant. Il vient \dresultat {\Delta = -1/4}, d'où les deux racines complexes conjuguées~: $$ z_A = {{1\over 2} - i {1\over 2}\over 2} \quad {\rm soit} \quad \dresultat {z_A = {1\over 4} - {1\over 4}i} \qquad {\rm et} \qquad \dresultat {z_B = {1\over 4} + {1\over 4}i}. $$ Et on vérifie ensuite que $$ {z_3\over z_1} = {i\over 2 + 2i} = {i (2 - 2i)\over (2 + 2i) (2 - 2i)} = {2i + 2\over 8} = {i + 1\over 4} = z_B, $$ ce qui prouve que \tresultat {$z_3/z_1$ est une solution de l'équation proposée}. \fincorrige