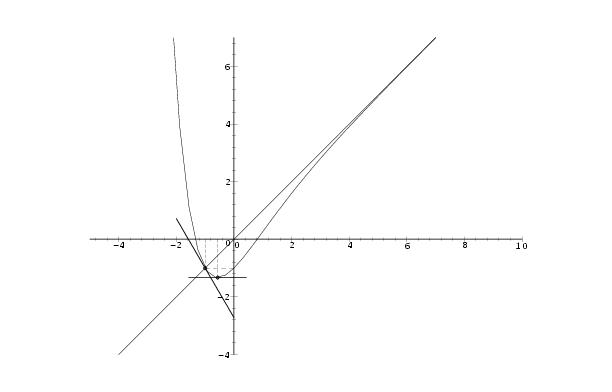
\exo{\'Etude d'une fonction exponentielle} \let \partie \centerpartie Le but du problème est l'étude de la fonction $f$ définie par $\displaystyle{ f (x) = x - {x+1 \over e^x} }$ et le calcul d'une aire. \medskip \partie{I} Soit $u$ la fonction numérique définie sur $\rset$ par $$ u (x) = e^x + x. $$ \itemnum Déterminer les limites de $u(x)$ quand $x$ tend vers $+\infty$ et quand $x$ tend vers $-\infty$. \'Etudier le sens de variation de $u$ et dresser son tableau de variation. \itemitemalphnum Démontrer que l'équation $e^x + x = 0$ n'admet sur $\rset$ qu'une solution unique, que l'on notera $\alpha$. \itemitemalph Démontrer que $\alpha$ appartient à $]-1,0[$. \itemitemalph Déterminer une valeur approchée de $\alpha$ à $10^{-3}$ près par défaut. \itemnum De l'étude précédente, déduire le signe de $u(x)$ sur chacun des intervalles $]-\infty,\alpha[$ et $]\alpha, +\infty[$. \partie{II} Soit $f$ la fonction numérique définie sur $\rset$ par $$ f (x) = x - {x+1 \over e^x}. $$ \itemnum Déterminer les limites de $f(x)$ quand $x$ tend vers $+\infty$ et quand $x$ tend vers $-\infty$. \itemitemalphnum Calculer $f'(x)$. \itemitemalph Démontrer que $f'(x)$ a le même signe que $u(x)$. \itemitemalph En déduire le sens de variation de la fonction $f$ et dresser son tableau de variation (on utilisera la valeur approchée de $\alpha$ trouvé au {\bf 2.} du {\bf I.} pour calculer une valeur approchée de $f(\alpha)$). \partie{III} On appelle $\cal C$ la représentation graphique de $f$ dans un repère orthonormal $(O,\vec \imath,\vec \jmath\,)$, unité~: 2~cm. \itemnum Démontrer que $\cal C$ admet la droite $D$ d'équation $y = x$ comme asymptote. \itemnum Soit $g$ la fonction numérique définie par $$ g (x) = f (x) - x. $$ \'Etudier le signe de $g(x)$ sur $\rset$ et en déduire la position de $\cal C$ par rapport à $D$. On précisera les coordonnées de leur point commun $I$. \itemnum Déterminer l'équation de la tangente $T$ à $\cal C$ en $I$. \itemnum Tracer avec soin dans le repère $(O,\vec \imath,\vec \jmath\,)$ les droites $T$ et $D$ ainsi que la courbe $\cal C$. \partie{IV} \itemnum Soit $h$ la fonction numérique définie sur $\rset$ par : $$ h (x) = (ax+b) e^{-x}. $$ \itemitemalph Déterminer les réels $a$ et $b$ de façon que la fonction $h$ soit une primitive de la fonction $g$. \itemitemalph En déduire une primitive $F$ de la fonction $f$. \itemnum Calculer la valeur exacte en cm$^2$, de l'aire de la partie $E$ du plan limitée par la courbe et les droites d'équations $y = 0$, $x = -1$ et $x = 0$. On donnera une valeur approchée de cette aire à $10^{-2}$ près par défaut. \finexo \corrige{} \let \partie \centerpartie \partie{I} \setbox \tmpbox = \vbox{% \eightpoint\rm \def \hfq{\hfil \ } \offinterlineskip \halign{ % preamble &\hfq #\hfq \cr $x$& \vrule depth 5pt & $-\infty$&& $+\infty$% \cr \noalign{\hrule} $u' (x)$& \vrule height 10pt depth 3pt && $+$ \cr \noalign{\hrule} \bbuucenter{$u (x)$}& \vrule& \down{$-\infty$}& \bbrightuuparrow & \bbuup{$+\infty$} \cr }} \rightillustrate{\tmpbox}{-6} % \num\ Comme $u (x) = e^x + x$, on a facilement $$ \dresultat{\lim_{x\rightarrow +\infty} u (x) = + \infty} \quad {\rm et} \quad \dresultat{\lim_{x\rightarrow -\infty} u (x)= - \infty}. $$ Et \mresultat{u' (x) = 1 + e^x} qui est toujours strictement positif puisque $e^x$ toujours positif. D'où le tableau de variations de $u$. \num\ Comme $u$ est une fonction strictement croissante et qu'elle change de signe sur $\rset$, on en déduit que l'équation $u (x) = 0$ \tresultat{admet une unique solution $\alpha$ sur $\rset$}. Et comme $u (-1) < 0$ et $u (0) > 0$, on peut même préciser que \mresultat{\alpha \in \, ]-1, 0[}. Avec la calculatrice, on affine l'encadrement par dichotomie pour obtenir $-0, 568 < \alpha < -0, 567$ (puisque $u (-0, 568) < 0$ et $u (-0, 567) > 0$), et la valeur approchée par défaut cherchée est \mresultat{\alpha \simeq -0, 568} \num\ On a donc finalement \tresultat{$u (x)$ négatif pour $x < \alpha$} et \tresultat{$u (x)$ positif pour $x > \alpha$} \partie{II} \begingroup \everymath = {\displaystyle } Beaucoup d'écritures possibles pour $f (x)$, par exemple~: $$ f (x) = x - {x+1 \over e^x} = x - {x \over e^x} - {1\over e^x} = x - xe^{-x} - e^{-x} = e^{-x} (xe^x - x - 1) = {xe^x - x- 1 \over e^x \ldots} $$ Le tout est de choisir la bonne, suivant l'utilisation que l'on veut en faire\dots \itemnum $\lim_{x \rightarrow +\infty} f (x) = \lim_{x \rightarrow +\infty} \Big( x - {x \over e^x} - {1\over e^x} \Big) = \lim_{x \rightarrow +\infty} \Big( \downto{x}{+\infty} - \downto{xe^{-x}}{0} - \downto{e^{-x}}{0} \Big) = $ \dresultat{+ \infty = \lim_{x \rightarrow +\infty} f (x)}. \item{} et $\lim_{x \rightarrow -\infty} f (x) = \lim_{x \rightarrow -\infty} \downto{e^{-x}}{+\infty} (\downto{xe^x}{0} \phantom{-} \downto{-x}{+\infty} - 1) =$ \dresultat{+ \infty = \lim_{x \rightarrow -\infty} f (x)}. \itemnum On a $$ f' (x) = 1 - {e^x - x e^x - e^x \over \big( e^x \big)^2} = 1 + {x \over e^x} = {e^x + x \over e^x} \qquad {\rm soit} \qquad \dresultat{f' (x) = {u (x) \over e^x}}, $$ ce qui prouve que \tresultat{$f' (x)$ est du signe de $u (x)$} car $e^x$ est toujours positif. D'où le tableau de variations de $f$~: $$\vcenter{ \eightpoint\rm \def \hfq{\hfil \ } \offinterlineskip \halign{ % preamble &\hfq #\hfq \cr $x$& \vrule depth 5pt & $-\infty$&& $\alpha$&& $+\infty$% \cr \noalign{\hrule} $f' (x)$& \vrule height 10pt depth 3pt && $-$& $0$& $+$ \cr \noalign{\hrule} \bbuucenter{$f (x)$}& \vrule& \bbuup{$+\infty$}& \bbrightddownarrow & \down{$\simeq -1, 33$}& \bbrightuuparrow & \bbuup{$+\infty$} \cr }} $$ On peut remarquer que l'on a $f (\alpha) = 1 + \alpha + {1\over \alpha}$ puisque $e^\alpha = -\alpha$ d'après le {\bf I. 2.}. \partie{III} \itemnum On a $\lim_{x \rightarrow +\infty} \big( f (x) - x \big) = \lim_{x \rightarrow +\infty} ( - x e^{-x} - e^{-x} ) = 0$ (car $\lim_{x \rightarrow +\infty} x e^{-x} = 0$ d'après le cours), donc $$ \tresultat{$D$ et $\cal C$ sont asymptotes en $+\infty$}. $$ \itemnum On a $g (x) = f (x) - x = -x e^{-x} - e^{-x} = -e^{-x} (x+1)$, donc $g (x)$ est du signe de $- (x+1)$ d'où les positions relatives~: $$\vcenter{ \eightpoint\rm \offinterlineskip \halign{ % preamble &\hfq #\hfq \cr $x$& \vrule depth 5pt & $-\infty$&& $-1$&& $+\infty$% \cr \noalign{\hrule} $f (x) - x$& \vrule height 10pt depth 3pt && $+$& $0$& $-$ \cr \noalign{\hrule} \tvi height 12pt positions& \vrule&& $C_f$ au dessus de $D$& \vrule & $C_f$ au dessous de $D$ \cr }} $$ En particulier, il n'y a qu'un seul point d'intersection~: \tresultat{le point $I (-1, -1)$}. \itemnum On a $f' (-1) = 1 - e$ et $f (1) = -1$ d'où la tangente cherchée \mresultat{T: \quad y = (1-e) x - e}. \def \epspath{% $HOME/tex_doc/lycee/database/term/sti/analyse/exp/} \itemnum $$ \superboxepsillustrate{pbm_002.ps} $$ \endgroup %% fin du \displaystyle pour \everymath \partie{IV} \itemalphnum On veut que $h$ soit une primitive de $g$. Autrement dit, on veut avoir $h' (x) = g (x)$. Comme $h' (x) = ae^{-x} - (ax+b) e^{-x} = e^{-x} (-ax + a-b)$ et que $g (x) = e^{-x} (-x-1)$ , on voit, par identification des coefficients, que l'on doit avoir $$ \cases{ -a = -1 \cr a-b = -1 \cr} \qquad {\rm soit} \qquad \mresultat{a= 1} \quad {\rm et} \quad \mresultat{b=2} $$ On en déduit qu'une primitive de $g$ est la fonction $h$ définie par \mresultat{h (x) = (x+2) e^{-x}}. \itemalph Et comme $f (x) = g (x) + x$, on en déduit qu'une primitive de la fonction $F$ est, par exemple, la fonction $F$ définie sur $\rset$ par \dresultat{F (x) = {x^2 \over 2} + (x+2) e^{-x}}. \itemnum Comme $f (-1) = -1$ et $f (0) = -1$, on en déduit, au vu du tableau de variations, que la fonction $f$ reste négative sur tout l'intervalle $[-1, 0]$. L'aire cherchée est donc donnée par le calcul $$ {\cal A} = - \int_{-1}^0 f (x) \, dx = - \big[ F (x) \big]_{-1}^0 = - \Big( 2 - {1\over2} - e \Big) = e - {3\over2} \quad \hbox{en unités d'aire} $$ L'unité d'aire étant de $2 \times 2 = 4$~cm$^2$, on en déduit que l'aire cherchée est de \tresultat{$(4e - 6)$~cm $^2$}, soit, à $10^{-2}$ près par défaut, \mresultat{{\cal A} \simeq 4, 873 \cm^2}. \fincorrige