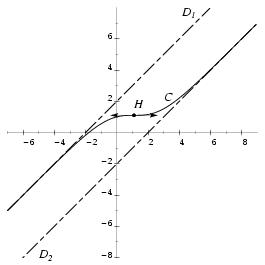
\exo {Un problème de synthèse avec l'exponentielle} {\rm problème p 53}, {\sl Anabac sti 2000, Nathan non corrigé} Le plan est rapporté à un repère orthonormal $(O, \vec \imath , \vec \jmath )$ (unité graphique~: $2\cm $ ou $2$~grands carreaux). \let \partie \centerpartie \partie {A} Soient $a$ et $b$ deux nombres réels. On désigne par $g$ la fonction définie sur $\rset $ par~: $$ g (x) = ax + b - {4e^x \over e^x + 3}. $$ \itemnum Calculer $g' (x)$. \itemnum Déterminer $a$ et $b$ pour que la courbe représentative de la fonction $g$ passe par le point $H$ et admette en ce point une tangente parallèle à l'axe des abscisses. \partie {B} On se propose d'étudier la fonction $f$ définie sur $\rset $ par $$ f (x) = x + 2 - {4e^x \over e^x + 3}. $$ \itemnum Vérifier que, pour tout réel $x$, on a~: $$ f (x) = x - 2 + {12 \over e^x + 3}. $$ \itemnum En utilisant l'une des deux écritures de $f (x)$, déterminer les limites de $f$ en $+\infty $ et en $-\infty $. \itemitemalphnum Démontrer que les droites $(D_1)$ et $(D_2)$ d'équations respectives $$ (D_1)~:\quad y = x-2 \qquad {\rm et} \qquad (D_2)~:\quad y = x+2 $$ sont asymptotes obliques à la courbe $C_f$ représentative de la fonction $f$. \itemitemalph Préciser la position de $C_f$ par rapport à chacune des droites $(D_1)$ et $(D_2)$. \itemitemalphnum Calculer $f' (x)$. \itemitemalph Montrer que $f' (x) \geq 0$ pour tout réel $x$. \itemitemalph En déduire le tableau de variation de la fonction $f$. \itemnum Construire les droites $(D_1)$, $(D_2)$ et la courbe $C_f$. \partie {C} \itemnum Déterminer une primitive de la fonction $h$ définie sur $\rset $ par $$ h (x) = {e^x \over e^x + 3}. $$ \itemnum En déduire la primitive de la fonction $h$ qui prend la valeur $2$ pour $x=0$. \finexo \corrige {} \let \partie \centerpartie \partie {A} \itemnum Il vient $$ g' (x) = a - {4 e^x (e^x+3) - 4e^x e^x \over \big( e^x + 3\big) ^2} \qquad {\rm soit} \qquad \dresultat {g' (x) = a - {12 e^x \over \big( e^x + 3\big) ^2}} $$ \itemnum Traduisons les hypothèses~: $C_g$ passe par $H$ si et seulement si $g (\ln 3) = \ln 3$, et la tangente en $H$ est horizontale si et seulement si $g' (\ln 3) = 0$. Or on a $$ g (\ln 3) = a\ln 3 + b - 2 \qquad {\rm et} \qquad g' (\ln 3) = a-1 $$ on a donc facilement \dresultat {a = 1} et \dresultat {b = 2}, soit \dresultat {g (x) = x+2 - {4e^x \over e^x + 3}}. \partie {B} \itemnum Il suffit de calculer la différence et de montrer qu'elle est nulle. Or $$ x+2 - {4e^x \over e^x + 3} - x + 2 - {12\over e^x + 3} = 4 - {4e^x + 12\over e^x + 3} = 0, $$ la dernière égalité étant obtenue par réduction au même dénominateur. On a donc finalement $$\dresultat { x - 2 + {12\over e^x +3} = f (x) = x + 2 - {4e^x\over e^x +3} }$$ \itemnum On trouve $$ \lim _{x\to +\infty } x - 2 + {12\over e^x +3} = \dresultat {+\infty = \lim _{x\to +\infty } f (x)} $$ puisque $\displaystyle { \lim _{x\to +\infty } x - 2 = +\infty }$, $\displaystyle { \lim _{x\to +\infty } e^x + 3 = +\infty }$ et $\displaystyle { \lim _{x\to +\infty } {12\over e^x + 3} = 0 }$. \item {} Et $$ \lim _{x\to -\infty } x + 2 - {4e^x\over e^x +3} = \dresultat {-\infty = \lim _{x\to -\infty } f (x)} $$ puisque $\displaystyle { \lim _{x\to -\infty } x + 2 = -\infty }$, $\displaystyle { \lim _{x\to -\infty } e^x + 3 = 3 }$ et $\displaystyle { \lim _{x\to -\infty } 4e^x = 0 }$. \itemnum En reprenant les calculs ci-dessus, on montre facilement que l'on a $$ \lim _{x\to -\infty } f (x) - (x+2) = \lim _{x\to -\infty } - {4e^x\over e^x +3} = 0 \qquad {\rm et} \qquad \lim _{x\to +\infty } f (x) - (x-2) = \lim _{x\to +\infty } {12e^x\over e^x +3} = 0 $$ Ainsi, \tresultat {les droites $D_1$ et $D_2$ sont asymptotes à la courbe $C$}. \item {} Quand aux positions relatives, il faut étudier le signe de ces différences. Une fois remarqué que $e^x$ était toujours positif, il devient évident, au vu des calculs précédents, que $f (x) - (x+2)$ est toujours négatif, alors que $f (x) - (x-2)$ est toujours positif. D'où les positions relatives~: \tresultat {$D_2$ toujours en dessous de $C$} et \tresultat {$D_1$ toujours en dessus de $C$} \itemnum Prenons la première expression de $f$, on trouve alors, en utilisant la formule $(1/u)' = -u'/u^2$, $$ f' (x) = 1 - {12e^x\over \big( e^x + 3\big) ^2} = {\big( e^x + 3\big) ^2 - 12e^x \over \big( e^x + 3\big) ^2} \qquad {\rm soit} \qquad \dresultat {f' (x) = {e^{2x} - 6e^x +9 \over \big( e^x + 3\big) ^2}} $$ et $f' (x)$ est du signe de $e^{2x} - 6x + 9$ puisque le dénominateur est toujours positif. \item {} Reste à voir que $e^{2x} - 6e^x + 9 = \big( e^x - 3\big) ^2$ pour pouvoir conclure que cette expression est toujours positive ou nulle, et qu'elle ne s'annulle que lorsque $e^x = 3$, c'est à dire quand $x = \ln 3$. \item {} Si on ne s'aperçoit pas immédiatement de l'identité remarquable, alors on va chercher le signe de l'expression $e^{2x} - 6e^x + 9$. Pour ce faire, on utilise le changement de variable $X = e^x$, qui implique $X^2 = e^{2x}$ et on calcule le discriminant $\Delta $ de l'expression $X^2 - 6X + 9$ pour trouver $\Delta = 0$, d'où la racine unique $X=3$ et la factorisation de l'expression en $(X-3)^2$\dots \item {} En résumé, on obtient le tableau suivant~: $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& -\infty && \ln 3&& +\infty \cr \noalign {\hrule height 1pt } f' (x)&& &+& 0& + \cr \noalign {\hrule height 1pt} \buucenter {$f (x)$}&& \down {$-\infty $}& \brightuparrow & \buucenter{$\ln 3$}& \bup {\brightuparrow }& \buup {$+\infty $} \cr }} }$$ \def \epspath {% $HOME/tex_doc/lycee/database/term/sti/analyse/exp/} \epsfxsize = 80mm \itemnum et le graphique~: $$ \superboxepsillustrate {pbm_008.ps} $$ \partie {C} \itemnum On reconnaît une expression de la forme $u'/u$, avec $u (x)$ toujours positif. Une primitive de la fonction $h$ est donc, par exemple, la fonction $H$ définie pour tout réel $x$ par \dresultat {H (x) = \ln (e^x + 3)}. \itemnum En reprenant l'expression $$ f (x) = x+2 - {4e^x \over e^x + 3}, $$ on voit que les primitives de la fonction $f$ sont toutes les fonctions $F$ qui s'écrivent $$ F (x) = {x^2 \over 2} + 2x - 4H (x) + k \qquad {\rm où} \qquad k \hbox { est une constante réelle quelconque} $$ Comme $H (0) =\ln 4$, et sachant que l'on veut avoir $F (0) = 2$, on voit qu'il faut prendre $k = 2 + 4\ln 4$. D'où la primitive cherchée~: $$ \dresultat {F (x) = {x^2 \over 2} + 2x - 4H (x) + 2 + 4\ln 4} $$ \fincorrige