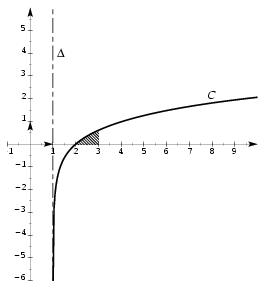
\exo {\' Etude d'une fonction comportant du logarithme et de l'exponentielle} \let \partie \centerpartie \partie {A -- \' Etude d'une fonction auxiliaire} Soit $g$ la fonction numérique de la variable réelle $x$ définie sur $]1; +\infty [$ par $$ g (x) = 1 - {x-1\over e^x}. $$ \itemnum Déterminer la valeur exacte de $g (2)$. \itemnum Calculer la limite de la fonction $g$ en $1$. \itemitemalphnum En remarquant que $$ g (x) = 1 - {x\over e^x} + {1\over e^x}, $$ calculer la limite de la fonction $g$ en $+\infty $. \itemitemalph Déduire de {\bf 3.}{\sl a\/}) que la courbe représentative de la fonction $g$ admet une asymptote horizontale en $+\infty $ , dont on précisera une équation. \itemitemalphnum On note $g'$ la fonction dérivée de la fonction $g$. Calculer $g' (x)$. \itemitemalph \' Etudier le signe de $g' (x)$ sur $]1; +\infty [$. \itemitemalph Dresser le tableau de variations de $g$. \itemitemalph En déduire le signe de $g (x)$ sur $]1; +\infty [$. (On ne demande pas de tracer la courbe représentative de la fonction $g$.) \partie {B -- \' Etude d'une fonction et tracé de sa courbe représentative} Soit $f$ la fonction de la variable réelle $x$ définie sur $]1; +\infty [$ par $$ f (x) = {1\over e^x} - {1\over e^2} + \ln (x-1). $$ On note $C$ la courbe représentative de la fonction $f$ dans un repère orthonormal $(O, \vec \imath , \vec \jmath \,)$, d'unité graphique $5\cm$. \itemitemalphnum Calculer la limite de la fonction $f$ en $1$. \itemitem {} En déduire l'existence d'une asymptote $\Delta $ à la courbe $C$, dont on précisera une équation. \itemitemalph Calculer la limite de $f$ en $+\infty $. \itemitemalphnum On note $f'$ la fonction dérivée de la fonction $f$. Calculer $f' (x)$. \itemitemalph Montrer que $$ f' (x) = {g (x)\over x-1}. $$ \itemitemalph En déduire le sens de variation de $f$ sur $]1; +\infty [$. Dresser la tableau de variation de $f$. \itemitemalphnum Calculer $f (2)$. \itemitemalph Tracer la droite $\Delta $ et la courbe $C$ dans le repère défini précédemment. \partie {C -- Calcul d'aire} On considère la fonction numérique $F$ de la variable réelle $x$ définie sur $]-1; +\infty [$ par $$ F (x) = - {1\over e^x} + (x-1) \ln (x-1) - \left( 1+ {1\over e^2}\right) x. $$ \itemnum Montrer que $F$ est une primitive de $f$ sur $]1;+\infty [$. \itemitemalphnum On désigne par $\cal A$ l'aire en $\cm ^2$ de la partie de plan limitée par la courbe $C$, l'axe des abscisses, les droites d'équations $x=2$ et $x=3$. \itemitem {} Déterminer la valeur exacte de $\cal A$. \itemitemalph Donner une valeur de $\cal A$ en $\cm ^2$ à $10^{-2}$ près. \finexo \corrige \let \partie \llappartie \partie {A} \vskip -5mm \itemnum On trouve \dresultat {g (2) = 1 - 1/e^2 = 1 - e^{-2}}$\approx 0,135$ \itemnum On a $$ \dresultat {\lim _{x\to 1} g (x) = 1} \qquad {\rm puisque} \qquad g (x) = 1 - {x-1\over e^x} \qquad {\rm avec} \qquad \lim _{x\to 1} (x-1) = 0 \quad {\rm et} \quad \lim _{x\to 1} {x-1\over e^x} = 0 $$ \itemalphnum Il est bien clair que l'on a $$\dresultat { 1 - {x-1\over e^x} = g (x) = 1 - {x\over e^x} + {1\over e^x}. }$$ d'où \dresultat {\lim _{x\to +\infty } g (x) = 1} puisque $$ g (x) = 1 - {x\over e^x} + {1\over e^x} \qquad {\rm avec} \qquad \lim _{x\to +\infty } e^x = +\infty \quad {\rm et} \quad \lim _{x\to +\infty } 1/e^x = 0 \quad {\rm et} \quad \lim _{x\to +\infty } x/e^x = 0 \quad {\rm (formulaire)} $$ \itemalph Le résulatt précédent signifie que la droite \tresultat {$y = 1$ est asymptote horizontale} en $+\infty $ à la courbe représentative de la fonction $g$. \itemalphnum Reprenons la première écriture de $g (x)$. Il vient $$ g' (x) = -{e^x - (x-1)e^x\over (e^x)^2} = {(x-2) e^x\over (e^x)^2} \qquad {\rm et} \qquad \dresultat {g' (x) = {x-2\over e^x}}. $$ \itemalph \alph \ Le signe de $g' (x)$ est alors celui de $(x-2)$ puisque $e^x$ est toujours strictement positif. D'où le tableau de variation~: $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& 1 && 2&& +\infty \cr \noalign {\hrule height 1pt } g' (x)&& &-& 0& + \cr \noalign {\hrule height 1pt} \buucenter {$g (x)$}&& \buup {1} & \brightddownarrow & \down {$\approx 0, 135$}& \brightuuparrow & \buup {$1$} \cr }} }$$ \itemalph Au vu du tableau de variation; il est clair que \tresultat {$g (x)$ est toujours positif} puisque son minimum est strictement positif. \partie {B} \vskip -5mm \itemalphnum On a \dresultat {\lim _{x\to 1} f (x) = -\infty } puisque $$ f (x) = {1\over e^x} - {1\over e^2} + \ln (x-1). \qquad {\rm avec} \qquad \lim _{x\to 1} 1/e^x = 1/e \quad {\rm et} \quad \lim _{x\to 1} {x-1} = 0 \quad {\rm et} \quad \lim _{x\to 1} {\ln (x-1)} = -\infty $$ On en déduit que la droite \tresultat {$\Delta $ d'équation $x=1$ est asymptote verticale} à la courbe $C$. \itemalph En $+\infty $, on a \dresultat {\lim _{x\to +\infty } f (x) = +\infty } puisque $$ f (x) = {1\over e^x} - {1\over e^2} + \ln (x-1). \qquad {\rm avec} \qquad \lim _{x\to +\infty } 1/e^x = 0 \quad {\rm et} \quad \lim _{x\to +\infty } {\ln (x-1)} = +\infty $$ \itemalphnum En utilisant les formules $(1/u)' = -u'/u^2$ et $(\ln u)' = u'/u$, il vient $$ f' (x) = {-e^x\over (e^x)^2} + {1\over x-1} = \dresultat {{-1\over e^x} + {1\over x-1} = f' (x)}. $$ \itemalph Or $$ {g (x)\over x-1} = {1\over x-1} - {x-1\over e^x (x-1)} = {1\over x-1} - {1\over e^x} \qquad {\rm d'où} \qquad \dresultat {f' (x) = {g (x)\over x-1}}. $$ \itemalph On a montré précédemment que $g (x)$ était toujours strictement positif sur l'intervalle considéré, donc $f' (x)$ est du signe de $(x-1)$, qui est toujours positif sur l'intervalle, d'où le tableau de variation~: $$\dresultat { \vcenter {\offinterlineskip \eightpoint \rm \def \cc#1{ \hfil #1 \hfil } \halign { % preamble \cc {$#$}& #\tv && \cc {$#$} \cr x&& 1 && +\infty \cr \noalign {\hrule height 1pt } f' (x)&& & +& \cr \noalign {\hrule height 1pt} \bucenter {$f (x)$}&& \down {$-\infty $} & \brightuparrow & \bup {$1$} \cr }} }$$ \itemalphnum On trouve \dresultat {f (2) = 0}. \def \epspath {% $HOME/tex_doc/lycee/database/term/sti/analyse/exp/} \itemalph $$ \superboxepsillustrate {pbm_010.ps} $$ \partie {C} \vskip -5mm \itemnum Calculons la dérivée de $F$. Il vient $$\eqalign { F' (x) &= {e^x\over (e^x)^2} + \ln (x-1) + {(x-1) \over (x-1)} - \left( 1+ {1\over e^2}\right) \cr &= {1\over e^x} + \ln (x-1) + 1 - 1 - {1\over e^2} \qquad {\rm soit} \qquad \dresultat {F' (x) = f (x)} \cr }$$ ce qui prouve que \tresultat {$F$ est une primitive de $f$}. \itemalphnum L'unité d'aire étant de $5\cm \times 5 \cm = 25\cm ^2$, il vient $$ {\cal A} = 25\times \int _2^3 f (x)\, dx = 25\times \Big[ F (x)\Big] _2^3 = 25\times \big( F (3) - F (2)\Big) \quad \hbox {soit, après calcul} \quad \dresultat {{\cal A} = 25 (2\ln 2 - e^{-3} -1)\cm ^2} $$ \itemalph D'où \dresultat {{\cal A} \approx 8,41\cm^2}. \fincorrige