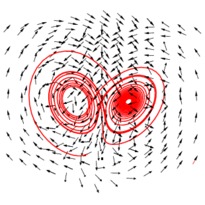
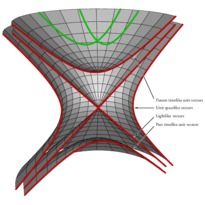
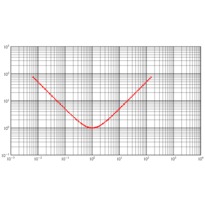
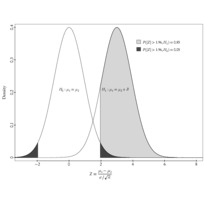
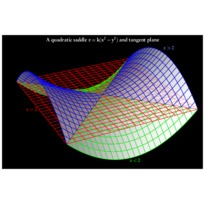
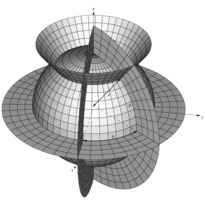
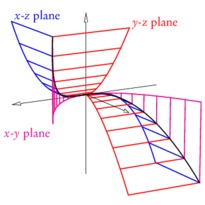
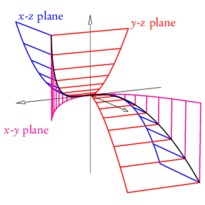
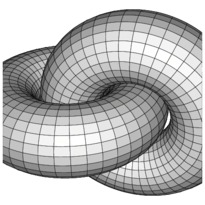
En cliquant sur une imagette, vous accéderez au source et à l'image. En cliquant sur cette dernière, vous ouvrirez le fichier PDF associé.

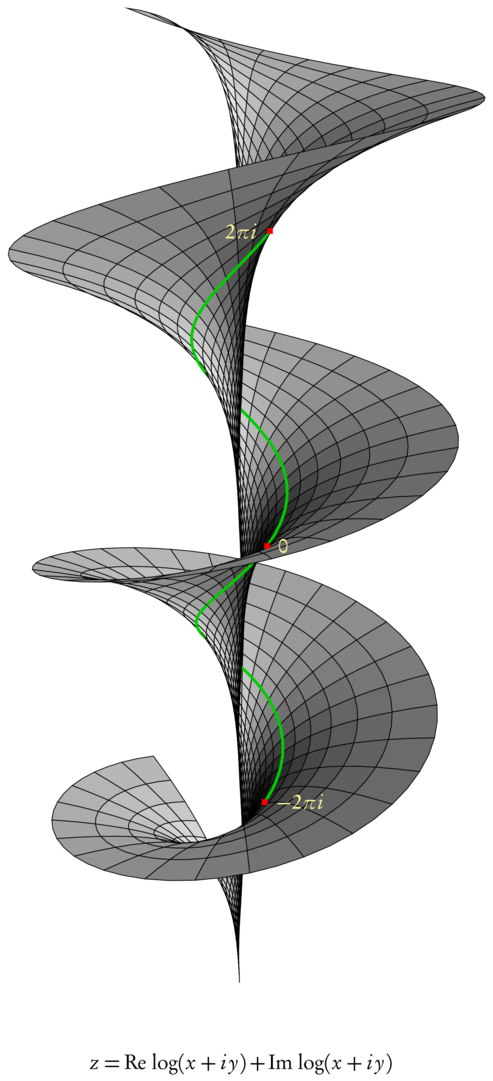
/* -*-ePiX-*- */ #include "epix.h" using namespace ePiX; // October 28, 2006 // // This file depicts two sheets of the Riemann surface of log, together // with the log function over the unit circle. Surface and path elements // must be drawn together. However, path-like mesh elements must be drawn // after surface elements that lie at the same location in the scene, // since otherwise surface elements' edges occlude the path. // // A mesh_elt class stores the necessary P data as well as a flag marking // the element as a segment or a surface patch. Elements are stored in a // std::vector (global to the scene) and sorted by distance. To ensure that // surface patches are printed first, their true distance is increased by a // "fudge" amount (0.25), making the By_distance class see them as farther // than they really are. // // Path elements are drawn in green; surface patches are shaded gray // according to the angle between the incoming light (from a point source) // and the surface normal. // // Surface patches are drawn as octagons to make the mesh appear smoother // than a quadrilateral mesh. The vertices of a patch are the images of the // corners and midpoints of a coordinate quadrilateral, "retracted" inward // by a small "gap" EPS (possibly zero). A positive gap simulates surface // transparency. // // (u,v+dv) (u+0.5*du,v+dv) (u+du,v+dv) // +----------------------+-----------------------+ // | *--------------------*---------------------* | // | | | | // | | | | // | | | | // + * (u+EPS,v+0.5*dv) * + (u+du,v+0.5*dv) // | | | | // | | | | // | | (u+EPS,v+EPS) | | // | *--------------------*---------------------* | // +----------------------+-----------------------+ // (u,v) (u+0.5*du,v) (u+du,v) const P LIGHT(2, 2, 0); // location of light, for shading const P VIEWPT(15,-10,6); // surface and path mesh fineness const int N1(18); const int N2(80); const int N3(120); const double du(4.5/N1); const double dv(6.0/N2); const double dt(4.0/N3); // "gap size" between surface mesh elements const double EPS(0); // (0.002); // visual styles void path_color() { green(0.8); } void label_color() { yellow(0.5); } void dot_color() { red(); } void path_width() { pen(1.5); } // class can represent either a surface element or a path element class mesh_elt { private: P pt1, pt2, pt3, pt4, pt5, pt6, pt7, pt8, center; double fudge; // artificial increment to distance static bool last_was_seg; bool is_segment; public: double how_far() const { return fudge + norm(center - camera.get_viewpt()); } mesh_elt(P f(double u, double v), double u0, double v0) : pt1(f(u0+EPS,v0+EPS)), pt2(f(u0+0.5*du,v0+EPS)), pt3(f(u0+du-EPS,v0+EPS)), pt4(f(u0+du-EPS,v0+0.5*dv)), pt5(f(u0+du-EPS,v0+dv-EPS)), pt6(f(u0+0.5*du,v0+dv-EPS)), pt7(f(u0+EPS,v0+dv-EPS)), pt8(f(u0+EPS,v0+0.5*dv)), center(0.25*(pt1 + (pt3 + (pt5 + pt7)))), fudge(0.25), is_segment(false) { } mesh_elt(P f(double), double t0) : pt1(f(t0)), pt2(f(t0+0.25*dt)), pt3(f(t0+0.5*dt)), pt4(f(t0+0.75*dt)), pt5(f(t0+dt)), pt6(), pt7(), pt8(), center(0.333*(pt1 + (pt3 + pt5))), fudge(0), is_segment(true) { } void draw() const { if (!is_segment) { P normal((pt2 - pt1)*(pt4 - pt1)); normal *= 1/norm(normal); double dens(0.5*(1-((normal|LIGHT)/norm(LIGHT)))); if (mesh_elt::last_was_seg) { mesh_elt::last_was_seg=false; plain(); // reset pen width } gray(dens); path temp(polygon(8, &pt1, &pt2, &pt3, &pt4, &pt5, &pt6, &pt7, &pt8)); temp.set_fill(); temp.draw(); epix_newline(); } else { // segment if (!mesh_elt::last_was_seg) { mesh_elt::last_was_seg=true; path_width(); path_color(); } start_path(); print(pt1); print(pt2); print(pt3); print(pt4); print(pt5); epix_newline(); } } // end of mesh_elt::draw() }; // end of class mesh_elt // initialize static data bool mesh_elt::last_was_seg = false; class By_distance { public: bool operator() (const mesh_elt arg1, const mesh_elt arg2) { return (arg1.how_far()) > (arg2.how_far()); } }; // the maps to be plotted P C_log(double u, double v) { return polar(exp(u), M_PI*v) + P(0, 0, u+M_PI*v); } P C_log1(double t) { return C_log(0,t); } int main() { bounding_box(P(-6, -12),P(6,12)); unitlength("1in"); picture(P(4,8)); begin(); fill(); degrees(); // label_angle(90); label(P(0, y_min), P(0,4), "$z=\\mathrm{Re}\\,\\log(x+iy) + \\mathrm{Im}\\,\\log(x+iy)$", t); radians(); // label_angle(0); viewpoint(VIEWPT); camera.range(20); std::vector<mesh_elt> mesh_data; // surface elements for (int i=0; i<N1; ++i) for (int j=0; j<N2; ++j) mesh_data.push_back(mesh_elt(C_log, -3+du*i, -3+dv*j)); // path elements for (int i=0; i<N3; ++i) mesh_data.push_back(mesh_elt(C_log1, -2+i*dt)); stable_sort(mesh_data.begin(), mesh_data.end(), By_distance()); for (int i=0; i<mesh_data.size(); ++i) mesh_data.at(i).draw(); dot_color(); marker(C_log(0,-2), BOX); marker(C_log(0, 0), BOX); marker(C_log(0, 2), BOX); label_color(); label(C_log(0,-2), P(6, 0), "$-2\\pi i$", r); label(C_log(0, 0), P(6, 0), "$0$", r); label(C_log(0, 2), P(-6, 0), "$2\\pi i$", l); end(); }