Fichier : pythagore1.mp
input constantes;
input geometriepoint;
beginfig(1);
u:=5mm;
affixe.B(u*(1,1))so;
affixe.C(z.B shifted(u*(sqrt(89),0)))se;
path cc;
cc=cercledia(B,C);
affixe.A(cc intersectionpoint cercle(C,8u))n;
affixe.D(z.A rotatedabout(z.B,90))so;
affixe.E(z.B rotatedabout(z.A,-90))no;
affixe.G(z.C rotatedabout(z.A,90))n;
affixe.F(z.A rotatedabout(z.C,-90))n;
affixe.H(z.B rotatedabout(z.C,90))se;
affixe.I(z.C rotatedabout(z.B,-90))so;
affixe.O(1/2[z.A,z.F])no;
affixe.K((z.A--z.G) intersectionpoint para(O,B,C,15));
affixe.L((z.C--z.F) intersectionpoint para(O,B,C,15));
affixe.M((z.A--z.C) intersectionpoint perpen(O,B,C,15));
affixe.N((z.F--z.G) intersectionpoint perpen(O,B,C,15));
picture piece[];
draw hachure(60,0.5,1);
clip currentpicture to (z.A--z.M--z.O--z.K--cycle);
piece1=currentpicture;
currentpicture:=nullpicture;
draw hachure(30,0.5,1);
clip currentpicture to (z.C--z.M--z.O--z.L--cycle);
piece2=currentpicture;
currentpicture:=nullpicture;
draw hachure(60,0.5,2);
clip currentpicture to (z.L--z.O--z.N--z.F--cycle);
piece3=currentpicture;
currentpicture:=nullpicture;
draw hachure(120,0.5,2);
clip currentpicture to (z.N--z.G--z.K--z.O--cycle);
piece4=currentpicture;
currentpicture:=nullpicture;
draw hachure(60,0.5,0);
clip currentpicture to (z.A--z.B--z.D--z.E--cycle);
piece5=currentpicture;
currentpicture:=nullpicture;
for j=1 upto 5:
draw piece[j];
endfor;
affixe.B(u*(1,1))so;
affixe.C(z.B shifted(u*(sqrt(89),0)))se;
path cc;
cc=cercledia(B,C);
affixe.A(cc intersectionpoint cercle(C,8u))n;
affixe.D(z.A rotatedabout(z.B,90))so;
affixe.E(z.B rotatedabout(z.A,-90))no;
affixe.G(z.C rotatedabout(z.A,90))n;
affixe.F(z.A rotatedabout(z.C,-90))n;
affixe.H(z.B rotatedabout(z.C,90))se;
affixe.I(z.C rotatedabout(z.B,-90))so;
affixe.O(1/2[z.A,z.F])no;
affixe.K((z.A--z.G) intersectionpoint para(O,B,C,15));
affixe.L((z.C--z.F) intersectionpoint para(O,B,C,15));
affixe.M((z.A--z.C) intersectionpoint perpen(O,B,C,15));
affixe.N((z.F--z.G) intersectionpoint perpen(O,B,C,15));
draw triangle(A,B,C);
draw codeperp(B,A,C,5);
draw z.B--z.D--z.E--z.A;
draw z.A--z.G--z.F--z.C;
draw z.C--z.H--z.I--z.B;
draw z.K--z.L;
draw z.M--z.N;
draw codeperp(N,O,L,5);
endfig;
end
|
 Une activité pour commencer
Une activité pour commencer Une activité pour commencer
Une activité pour commencer La figure
La figure
 Visualisation
Visualisation Vers le théorème de Pythagore
Vers le théorème de Pythagore Le Cours
Le Cours
 Applications
Applications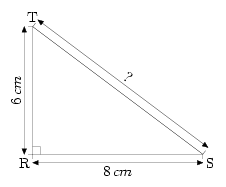
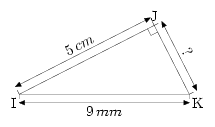
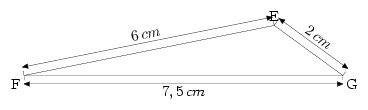
 Les exercices
Les exercices