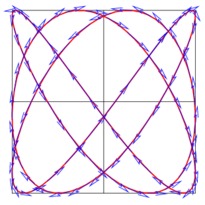
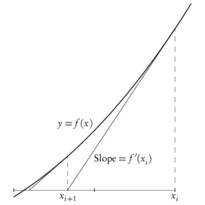
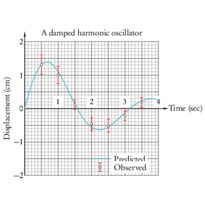
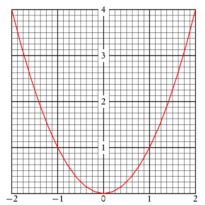
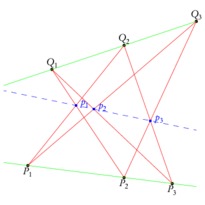
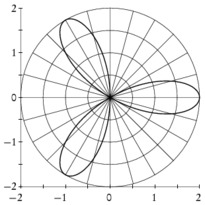
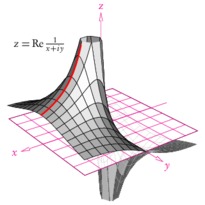
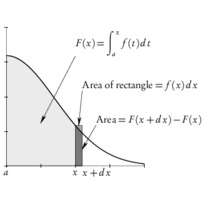
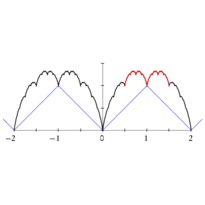
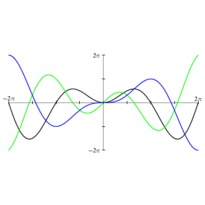
En cliquant sur une imagette, vous accéderez au source et à l'image. En cliquant sur cette dernière, vous ouvrirez le fichier PDF associé.
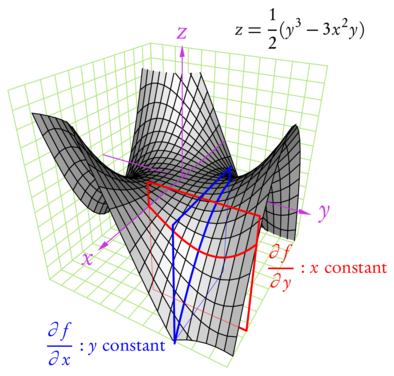
/* -*-ePiX-*- */ /* * ePiX surface demo image, June 08, 2006 * * This file illustrates the use of pstricks (for color-filled * arrowheads), manual layering of figure elements (for hidden-surface * removal), and simulated transparency. */ #include "epix.h" using namespace ePiX; // Style parameters // camera location (in spherical coordinates); must be in first orthant const P VIEWPT=sph(4, M_PI/6, M_PI/6); // colors void color_coord(void) { rgb(0.7, 0.9, 0.5); } void color_axis(void) { rgb(0.8, 0.2, 0.9); } void color_xslice(void) { red(); } void color_yslice(void) { blue(); } void ps_axis_color(void) { std::cout << "\n\\newrgbcolor{axis_color}{0.8 0.2 0.9}%"; } const int MESH(12); // number of coordinate grid squares // location of tangency point const double x_0=7.0/MESH; const double y_0=6.0/MESH; const double z_0=0.25; // height of top of slicing planes const int MAX=1; // maximum coordinate // function to be graphed P f(double x, double y) { return P(x, y, 0.75*y*(y*y-3*x*x)); } // constant y slice of the graph of f P Df_x(double t) { return f(t+x_0, y_0); } // constant x slice of the graph of f P Df_y(double t) { return f(x_0, t+y_0); } int main() { bounding_box(P(-2,-2), P(2,1)); picture(2,1.5); unitlength("1.25in"); use_pstricks(); begin(); viewpoint(VIEWPT); use_pstricks(false); clip_box(P(-2, -2, -1), P(2, 2, 0.75)); // front and back halves domain R1(P(-1,-1), P(0, 1), mesh(MESH, 2*MESH), mesh(MESH, 2*MESH)); domain R2(P( 0,-1), P(1, 1), mesh(MESH, 2*MESH), mesh(MESH, 2*MESH)); // coordinate grids color_coord(); grid(P(-MAX,-MAX,-MAX), P(-MAX, MAX, MAX), MESH, MESH); grid(P(-MAX,-MAX,-MAX), P( MAX,-MAX, MAX), MESH, MESH); grid(P(-MAX,-MAX,-MAX), P( MAX, MAX,-MAX), MESH, MESH); color_axis(); label(P(0,0.25+MAX,0), P(4,0), "$y$", r); label(P(0,0,0.25+MAX), P(0,4), "$z$", t); clip(); fill(); surface(f, R1); fill(false); clip(false); // coordinate axes bold(); use_pstricks(); ps_axis_color(); psset("linecolor=axis_color,fillcolor=axis_color"); // color_axis(); dart(P(0,-MAX,0), P(0,0.25+MAX,0)); dart(P(0,0,0), P(0,0,0.25+MAX)); use_pstricks(false); // vertices of slicing planes P pt1(x_0, 0, z_0), pt2(x_0, 0, -MAX), pt3(x_0, MAX, -MAX); P pt4(0, y_0, z_0), pt5(0, y_0, -MAX), pt6(MAX, y_0, -MAX); P pt7(x_0, 0, 0), pt8(x_0, MAX, z_0), pt9=f(0,y_0); P pt10(MAX, y_0, z_0); // lower outlines of slicing planes (partially hidden by surface) color_xslice(); polyline(3, &pt1, &pt2, &pt3).draw(); color_yslice(); polyline(3, &pt4, &pt5, &pt6).draw(); plain(); clip(); fill(); // front 1/2 of surface (x>0) surface(f, R2); fill(false); clip(false); // last coordinate axis bold(); use_pstricks(); psset("linecolor=axis_color, fillcolor=axis_color"); dart(P(-MAX,0,0), P(0.25+MAX,0,0)); use_pstricks(false); color_axis(); label(P(0.25+MAX,0,0), P(-2,-2), "$x$", bl); font_size("scriptsize"); // slices of the graph and labels pen(1); color_yslice(); plot(Df_x, -x_0, MAX-x_0, 20); label(Df_x(MAX-x_0), P(-4,0), "$\\displaystyle\\frac{\\partial f}{\\partial x}$: $y$ constant", l); clip(); color_xslice(); plot(Df_y, -y_0, MAX-y_0, 20); clip(false); label(Df_y(MAX-y_0), P(4,0), "$\\displaystyle\\frac{\\partial f}{\\partial y}$: $x$ constant", br); // overall label black(); label(P(-MAX, 0, MAX), P(2,2), "$z=\\displaystyle\\frac{1}{2}(y^3-3x^2y)$", tr); // fake transparency: redraw slicing planes thinly // clip(); pen(0.15); color_xslice(); rect(P(x_0, 0, -MAX), P(x_0, 1, z_0)); color_yslice(); rect(P(0, y_0, -MAX), P(1, y_0, z_0)); // upper outlines of slicing planes (not hidden by surface) bold(); color_xslice(); polyline(4, &pt7, &pt1, &pt8, &pt3).draw(); color_yslice(); polyline(4, &pt9, &pt4, &pt10, &pt6).draw(); end(); }