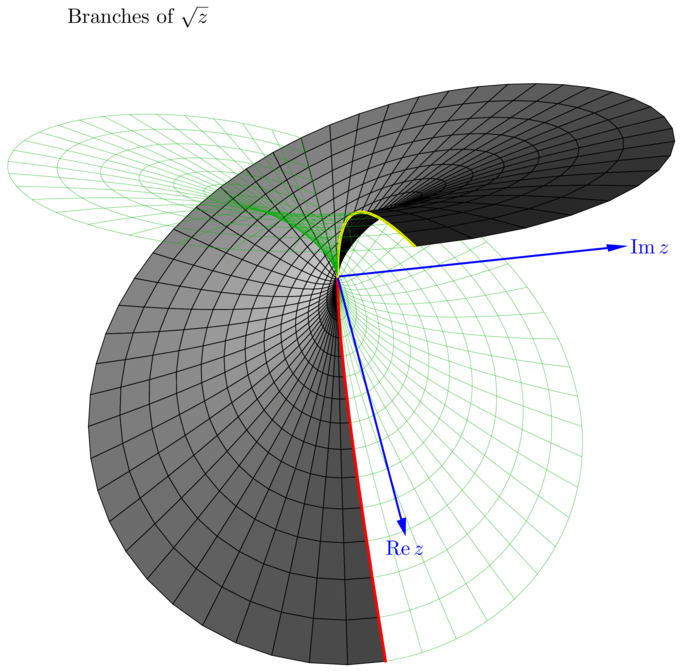
En cliquant sur une imagette, vous accéderez au source et à l'image. En cliquant sur cette dernière, vous ouvrirez le fichier PDF associé.


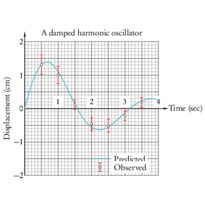
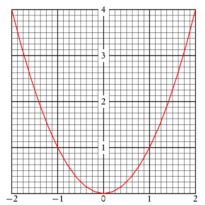
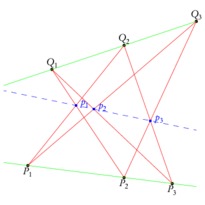
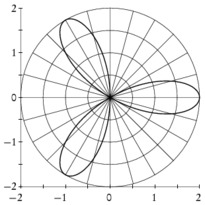
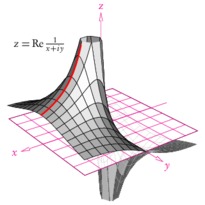
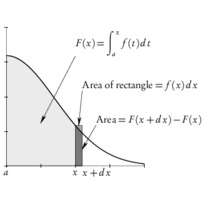

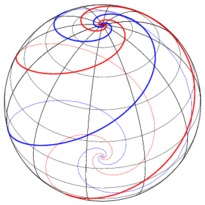
/* -*-ePiX-*- */ #include <stdio.h> #include "epix.h" using namespace ePiX; // radius of plot const double MAX=1.25; const double SQMAX=sqrt(MAX); // fineness of mesh grid const int N1=12*MAX; const int N2=48; const double du=SQMAX/N1, dv=1.0/N2; // parameter steps for solid surface const P LIGHT(1, -3, 1); // location of light, for shading const P VIEWPT(6,-1,5); class mesh_quad { private: P pt1, pt2, pt3, pt4; double ht; double distance; public: mesh_quad() { pt1=P(); pt2=P(); pt3=P(); pt4=P(); ht=0; distance=0; } mesh_quad(P f(double u, double v), double u0, double v0) { pt1=f(u0,v0); pt2=f(u0+du,v0); pt3=f(u0+du,v0+dv); pt4=f(u0,v0+dv); P center = 0.25*(pt1 + pt2 + pt3 + pt4); P temp = camera.get_viewpt(); ht=center.x3(); distance = norm(center-temp); } double how_far() const { return distance; } double height() const { return ht; } void draw() { P normal = (pt2 - pt1)*(pt4 - pt1); normal *= 1 / (norm(normal)+0.00005); double dens = 0.125+0.8*(1-pow((normal|LIGHT), 2)/(LIGHT|LIGHT)); gray(dens); quad(pt1, pt2, pt3, pt4); } }; // end of mesh_quad class // sorting criterion class by_distance { public: bool operator() (const mesh_quad& arg1, const mesh_quad& arg2) { return arg1.how_far() > arg2.how_far(); } }; // complex square root in polar coordinates P sqrt(double u, double v) { return polar(u*u, v) + P(0,0,u*Cos(0.5*v)); } // restrictions of sqrt to real axis, unit circle P sqrt_re(double t) { return sqrt(t,0); } P sqrt_im(double t) { return sqrt(1,t); } main() { bounding_box(P(-MAX, -MAX), P(MAX, MAX)); unitlength("1in"); picture(4,4); use_pstricks(); begin(); use_pstricks(false); revolutions(); label(P(x_min, y_max), P(2,-2), "Branches of $\\sqrt{z}$", br); viewpoint(VIEWPT); camera.range(4); circle C1 = circle(); // unit circle std::vector<mesh_quad> mesh(N1*N2); // list of mesh_quads // fill list, sort by distance to the camera for (int i=0; i<N1; ++i) for (int j=0; j<N2; ++j) mesh.at(N2*i+j) = mesh_quad(sqrt, du*i, dv*j); sort(mesh.begin(), mesh.end(), by_distance()); // draw bottom half of transparent branch pen(0.15); green(0.7); plot(sqrt, domain(P(0,1), P(SQMAX,1.5), Net(N1, 0.5*N2), Net(4*N1, 2*N2))); plain(); fill(); // draw bottom half of opaque branch for (int i=0; i<N1*N2; ++i) if (mesh.at(i).height() < 0) mesh.at(i).draw(); fill(false); // boundary curve, unit circle, axes, grid, labels pen(1.5); red(); plot(sqrt_re, -SQMAX, 0, 30); use_pstricks(); // for colored arrows psset("linewidth=1pt, linecolor=blue, fillcolor=blue"); arrow(P(0,0,0), P(MAX*1.1,0,0)); arrow(P(0,0,0), P(0,MAX*1.1,0)); use_pstricks(false); blue(); label(P(MAX*1.1,0,0), P(0,-4), "$\\mathrm{Re}\\,z$", b); label(P(0,MAX*1.1,0), P(4, 0), "$\\mathrm{Im}\\,z$", r); // draw top half of opaque branch black(); plain(); fill(); for (int i=0; i<N1*N2; ++i) if (mesh.at(i).height() >= 0) mesh.at(i).draw(); fill(false); pen(1.5); yellow(); plot(sqrt_re, 0, SQMAX, 30); pen(0.15); green(0.7); plot(sqrt, domain(P(0,1.5), P(SQMAX,2), Net(N1, 0.5*N2), Net(4*N1, 2*N2))); end(); }